Regression

Machine Learning

​ 第一堂课 是要简单跟大家介绍一下machine learning还有deep learning的基本概念，等一下会讲一个跟宝可梦完全没有关係的故事。想必大家在报章杂志上其实往往都已经听过机器学习这一个词汇，那你可能也知道说机器学习就是跟今天很热门的AI好像有那么一点关联。

​ 那所谓的机器学习到底是什么呢？顾名思义，机器他具备有学习的能力，那些科普文章往往把机器学习这个东西吹得玄之又玄好像机器会学习以后，我们就有了人工智慧，有了人工智慧以后机器接下来就要统治人类了。那机器学习到底是什么呢？事实上，机器学习概括来说可以用一句话来描述机器学习这件事，==机器学习就是让机器具备找一个函式的能力==。

​ 那机器具备找函式的能力以后,他确实可以做很多事 举例来说

1. 假设你今天想要叫机器做语音辨识,机器听一段声音,產生这段声音对应的文字,那你需要的就是一个函式,这个函式的输入是声音讯号,输出是这段声音讯号的内容。那你可以想像说 这个可以把声音讯号,当作输入文字当作输出的函式,显然非常非常的复杂，他绝对不是,你可以用人手写出来的方程式,这个函式他非常非常的复杂,人类绝对没有能力把它写出来,所以我们期待凭藉著机器的力量,把这个函式自动找出来，这件事情,就是机器学习。

​ 2. 还有好多好多的任务,我们都需要找一个很复杂的函式,举例来说 假设我们现在要做,影像辨识 那这个影像辨识,我们需要什麼样的函式呢？这个函式的输入是一张图片,他的输出是什麼呢？他是这个,图片裡面 有什麼样的内容。

​ 3. 或者是大家都知道的AlphaGo,其实也可以看作是一个函式,要让机器下围棋 我们需要的,就是一个函式 这个函式的输入,是棋盘上黑子跟白子的位置,输出是什麼 输出是机器下一步,应该落子的位置 假设你可以,找到一个函式 这个函式的输入,就是棋盘上黑子跟白子的位置,输出就是下一步应该落子的位置,那我们就可以让机器做自动下围棋,这件事 就可以做一个AlphaGo。

Different types of Functions

​ 随著我们要找的函式不同,机器学习有不同的类别,那这边介绍几个专有名词给大家,认识一下 第一个专有名词,叫作==Regression==,Regression的意思是说,假设我们今天要找的函式,他的输出是一个数值,他的输出是一个 scalar,那这样子的机器学习的任务,我们称之為Regression。

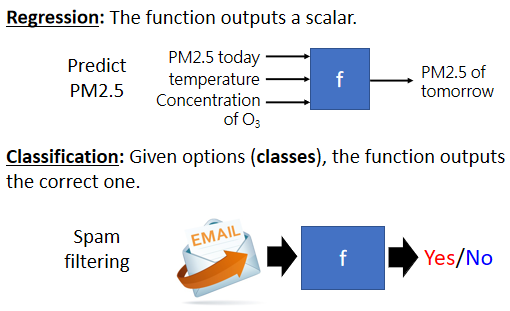
​ 那这边举一个Regression的例子,假设我们今天要机器做的事情,是预测未来某一个时间的,PM2.5的数值 你要叫机器,做的事情是找一个函式,这个我们用f来表示,这个函式的输出,是明天中午的PM2.5的数值,他的输入可能是种种跟预测PM2.5,有关的指数 包括今天的PM2.5的数值,今天的平均温度,今天平均的臭氧浓度等等,这一个函式可以拿这些数值当作输入,输出明天中午的PM2.5的数值,那这一个找这个函式的任务,叫作Regression。

​ 除了Regression以外,另外一个大家耳熟能详的任务,叫作==Classification==,那Classification这个任务,要机器做的是选择题 我们人类,先準备好一些选项 那这些选项,又叫作类别 又叫作classes,我们现在要找的函式它的输出,就是从我们设定好的选项裡面,选择一个当作输出 那这个问题,这个任务就叫作Classification。举例来说,现在每个人都有gmail account,那gmail account裡面有一个函式,这个函式可以帮我们侦测一封邮件,是不是垃圾邮件,这个函式的输入是一封电子邮件,那他的输出是什麼呢,你要先準备好你要机器选的选项,在侦测垃圾邮件这个问题裡面,可能的选项就是两个,是垃圾邮件 或不是垃圾邮件,Yes或者是No,那机器要从Yes跟No裡面,选一个选项出来,这个问题叫作Classification,那Classification不一定只有两个选项,也可以有多个选项 。

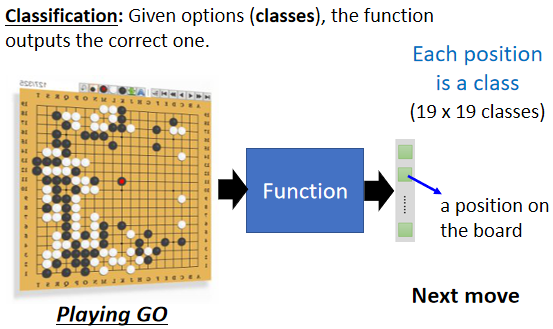
​ 举例来说,alpha go本身也是一个Classification,的问题 那只是这个Classification,他的选项是比较多的,那如果要叫机器下围棋,你想做一个 alpha go的话,我们要给机器多少的选项呢,你就想想看 棋盘上有多少个位置,那我们知道棋盘上有19乘19个位置,那叫机器下围棋这个问题 其实,就是一个有19乘19个选项的选择题,你要叫机器做的就是找一个函式,这个函式的输入是棋盘上,黑子跟白子的位置,输出就是从19乘19个选项裡面,选出一个正确的选项,从19乘19个可以落子的位置裡面,选出下一步应该要落子的位置,那这个问题也是一个分类的问题。

​ 其实很多教科书 在讲机器学习的,种种不同类型的任务的时候,往往就讲到这边 告诉你说,机器学习 两大类任务,一个叫作Regression,一个叫作Classification,然后就结束了,但是假设你对机器学习的认知,只停留在机器学习就是两大类任务,Regression跟Classification,那就好像你以為说,这个世界只有五大洲一样。

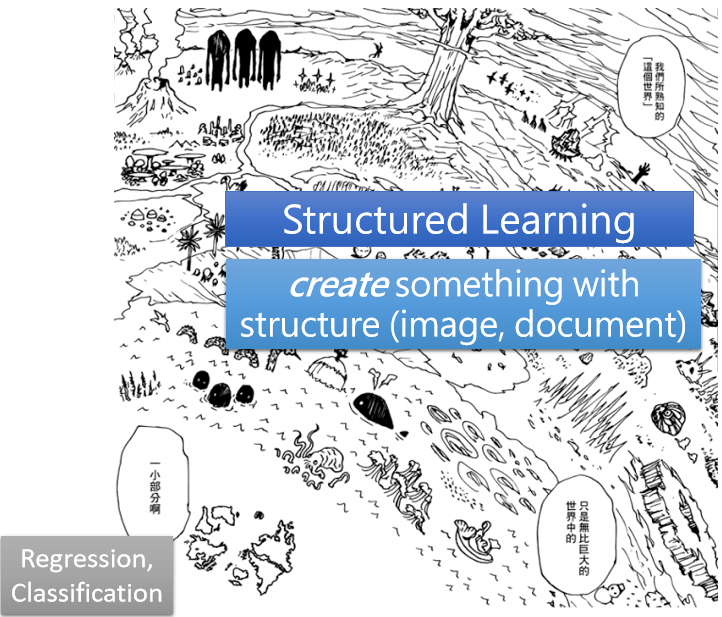
​ 你知道这个世界不是只有五大洲,这个世界外面是有一个,黑暗大陆的 这鬼灭之刃连载之前,我们就已经出发前往黑暗大陆了,鬼灭之刃连载以后,我们居然都还没有到,可见这个黑暗大陆距离那麼远,那在机器学习这个领域裡面,所谓的黑暗大陆是什麼呢,在於Regression跟Classification以外,大家往往害怕碰触的问题,叫作Structured Learning,也就是机器今天不只是要做选择题,不只是输出一个数字 还要產生,一个有结构的物件 举例来说,机器画一张图 写一篇文章,这种叫机器產生有结构的东西的问题,就叫作Structured Learning,那如果要讲得比较拟人化,比较潮一点 Structured Learning,你可以用拟人化的讲法说,我就是要叫机器学会创造这件事情,好那到目前為止,我们就是讲了三个机器学习的任务,Regression Classification跟Structured Learning,

Case Study

​ 我们说,机器学习就是要找一个函式,那机器怎麼找一个函式呢,那这边要用个例子跟大家说明说。在讲这个例子之前 先跟大家说一下,说这一门课有一个youtube的频道https://www.youtube.com/c/HungyiLeeNTU,然后这个我会把上课的录影,放到这个youtube的频道上面,那这个频道 感谢过去修过这门课的,同学不嫌弃 其实也蛮多人订阅,所以我算是一个三流的youtuber,是没有什麼太多流量,但是这边也是有7万多订阅。

​ 那為什麼突然提到,这个youtube的频道呢,因為我们等一下要举的例子,跟youtube是有关係的,youtuber在意的,就是这个频道的流量,假设有一个youtuber,是靠著youtube维生的,他会在意频道有没有流量,这样他才会知道他可以获利多少,假设你自己有youtube频道的话,你会知道说在youtube后台,你可以看到很多相关的资讯,你可以看到很多相关的资讯,比如说每一天按讚的人数有多少,每一天订阅的人数有多少,每一天观看的次数有多少,我们能不能够根据,一个频道过往所有的资讯去预测,它明天有可能的观看的次数是多少呢,我们能不能够找一个函式,这个函式的输入是youtube上面,youtube后台是我的资讯,输出就是某一天,隔天这个频道会有的总观看的次数.

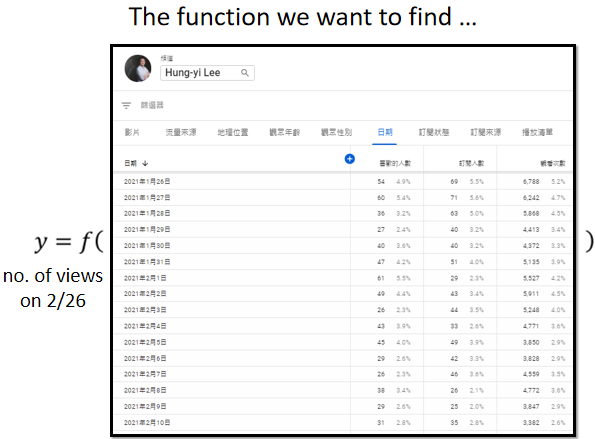
机器学习找这个函式的过程,分成三个步骤,那我们就用Youtube频道,点阅人数预测这件事情,来跟大家说明这三个步骤,是怎麼运作的

1. Function with Unknown Parameters

​ 第一个步骤是我们要==写出一个,带有未知参数的函式==,简单来说就是 我们先猜测一下,我们打算找的这个函式$F$,它的数学式到底长什麼样子。举例来说,我们这边先做一个最初步的猜测,我们写成这个样子

$$y=b+w\ast x_l$$

​ 这边的每一个数值是什麼呢,这个y啊 就假设是今天吧,不过今天还没有过完,所以我还不知道,今天总共的点阅次数是多少,所以这件事情是我们未知的,

• $y$是我们準备要预测的东西,我们準备要预测的是今天,2月26号这个频道总共观看的人
• $x_l$是这个频道,前一天总共观看的人数,$y$跟$x_l$都是数值,
• b跟w是未知的参数,它是準备要透过资料去找出来的,我们还不知道w跟b应该是多少,我们只是隐约的猜测

​ 这个猜测往往就来自於,你对这个问题本质上的了解,也就是Domain knowledge,所以才会听到有人说,这个做机器学习啊,就需要一些Domain knowledge,.

​ 所以我们这个能够预测未来点阅次数的函式$F$,它就一定是前一天的点阅次数,乘上w 再加上b呢,我们先不知道 这是一个猜测,也许我们觉得说,这个今天的点阅次数,总是会跟昨天的点阅次数有点关联,所以我们把昨天的点阅次数,乘上一个数值,但是总是不会一模一样,所以再加上一个b做修正,当作是对於2月26号,点阅次数的预测,这是一个猜测,它不一定是对的,我们等一下回头会再来修正这个猜测。

​ 那现在总之,我们就随便猜说,$y=b+w\ast x_l$,而b跟w是未知的,这个带有未知的==参数==,这个Parameter中文通常翻成参数,==这个带有Unknown的Parameter的Function 我们就叫做Model==,所以我们常常听到有人说,模型 Model,Model这个东西在机器学习裡面,就是一个带有,未知的Parameter的Function,

​ 这个$x_l$是这个Function裡面我们已知的,已经知道的东西,它是来自於Youtube后台的资讯,我们已经知道2月25号,点阅的总人数是多少,这个东西叫做==Feature==,而$w$跟$b$是我们不知道的,它是Unknown的Parameter,那这边我们也给$w$跟$b$,给他一个名字,这个跟Feature做相乘的未知的参数,这个w 我们叫它==weight==,这个没有跟Feature相乘的,是直接加下去的,这个我们叫它==Bias==,那这个只是一些名词的定义而已,等一下我们讲课的时候,我们在称呼,模型裡面的每一个东西的时候,会更為方便,好那这个是第一个步骤.

2. Define Loss from Training Data

​ 第二个步骤,是我们要==定义一个东西叫做Loss==,Loss它也是一个Function,那这个Function它的输入,是我们Model裡面的参数,我们的Model叫做,$y=b+w\ast x_l$,而$b$跟$w$是未知的,是我们準备要找出来的,所谓的这个Loss啊,它是一个Function,这个Function的输入,就是$b$跟$w$,所以L它是一个Function,它的输入是Parameter,是model裡面的Parameter,那这个Loss 这个Function,这个Function输出的值代表说,现在如果我们把这一组未知的参数,设定某一个数值的时候,这笔数值好还是不好。

​ 那这样讲可能你觉得有点抽象,所以我们就举一个具体的例子,假设现在我们给未知的参数的设定是$b$,这bias等於0.5k,这个$w$呢直接等於1,那这个Loss怎麼计算呢,如果我们b设0.5k,这个$w$设1,那我们拿来预测,未来的点阅次数的函式 就变成,y等於0.5k加1倍的xₗ,那这样子的一个函式,这个0.5k跟1,他们所代表的这个函式,它有多少呢,这个东西就是Loss.

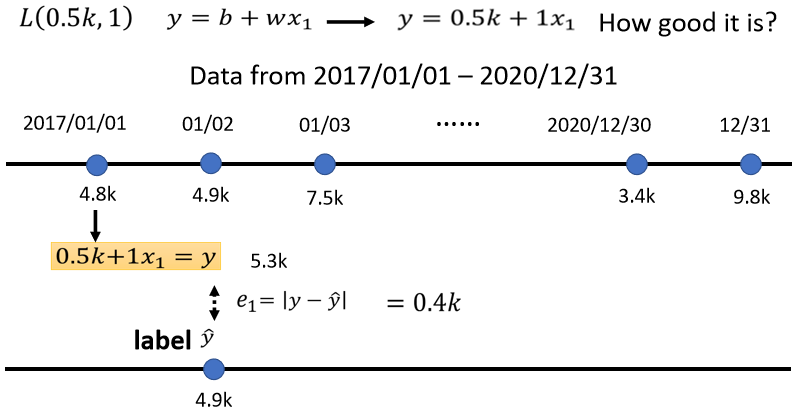
​ 我们要怎麼计算这个Loss呢,这个我们就要==从训练资料来进行计算==,在这个问题裡面,我们的训练资料是,这一个频道过去的点阅次数,举例来说,从2017年到2020年的点阅次数,每天的这个频道的点阅次数都知道,这边是假的数字啦,随便乱编的,好 所以那我们知道,2017年1月1号,到2020年12月31号的,点阅数字是多少,接下来我们就可以计算Loss。

​ 我们把2017年1月1号的点阅次数,代入这一个函式裡面,我们已经说我们想要知道,b设定為0.5k,$w$设定為1的时候,这个函式有多棒,当b设定為0.5k,w设定為1的时候,我们拿来预测的这个函数,是y等於0.5k加一倍的xₗ,那我们就把这个xₗ代4.8k,看它的预测出来的结果是多少,所以 根据这一个函式,根据$b$设0.5k,w设1的这个函式,如果1月1号,是4.8k的点阅次数的话,那隔天应该是4.8k乘1加0.5k,就是5.3k的点阅次数,那隔天实际上的点阅次数,1月2号的点阅次数我们知道吗,从后台的资讯裡面 我们是知道的,所以我们可以比对一下,现在这个函式预估的结果,跟真正的结果,它的差距有多大,这个函式预估的结果是5.3k,真正的结果是多少呢,真正的结果是4.9k,那这个真实的值叫做==Label==,它是高估了,高估了这个频道可能的点阅人数,那就可以计算一下这个差距,计算一下估测的值,跟真实的值的差距,这边估测的值用y来表示,真实的值用ŷ来表示,你可以计算y跟ŷ之间的差距,得到一个eₗ,代表估测的值跟真实的值之间的差距,那计算差距其实不只一种方式,我这边把y跟ŷ相减,直接取绝对值,算出来的值是0.4k。

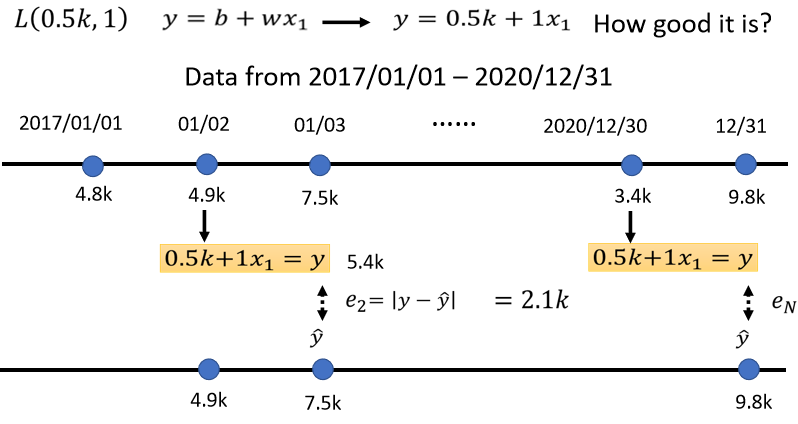
​ 那我们不是只能用1月1号,来预测1月2号的值,我们可以用1月2号的值,来预测1月3号的值,如果我们现在的函式是,y等於0.5k加一倍的xₗ,那1月2号,根据1月2号的点阅次数,预测的1月3号的点阅次数的,值是多少呢 是5.4k,以xₗ代4.9k进去,乘1在加0.5k 等於5.4k,接下来计算这个5.4k,跟真正的答案,跟Label之间的差距,Label是7.5k,看来是一个低估,低估了这个频道,在1月3号的时候的点阅次数,才可以算出e₂,这个e₂是,y减y跟ŷ之间的差距,算出来是2.1k,那同一个方法,你就可以算过这三年来,每一天的预测的误差,假设我们今天的Function,是y等於0.5k加一倍的xₗ,这三年来每一天的误差,通通都可以算出来,每一天的误差都可以给我们一个小e,

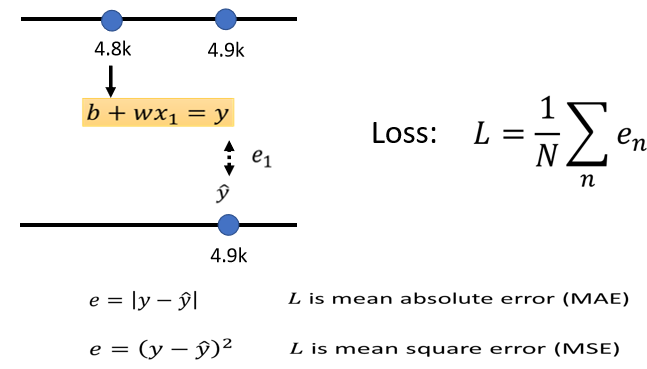
​ 接下来我们就把每一天的误差,通通加起来,加起来然后取得平均,这个大N代表我们的训验资料的个数,,就是三年来的训练资料,就365乘以3,每年365天 所以365乘以3,那我们算出一个L,我们算出一个大L,这大L是每一笔训练资料的误差,这个e相加以后的结果,这个大L就是我们的Loss.

==大L越大,代表我们现在这一组参数越不好,这个大L越小,代表现在这一组参数越好==

​ 估测的值跟实际的值之间的差距,其实有不同的计算方法,在我们刚才的例子裡面,我们是算y跟ŷ之间,绝对值的差距,这一种计算差距的方法,得到的这个大L,得到的Loss叫 mean absolute error,缩写是MAE,如果你今天的e是用,相减y平方算出来的,这个叫mean square error,又叫MSE,那MSE跟MAE,他们其实有非常微妙的差别.我们就是选择MAE,作為我们计算这个误差的方式,把所有的误差加起来,就得到Loss,那你要选择MSE也是可以的,在作业裡面我们会用MSE,那有一些任务,如果y和ŷ它都是机率,都是机率分佈的话,在这个时候,你可能会选择Cross-entropy,这个我们都之后再说,我们这边就是选择了MAE,那这个是机器学习的第二步.

Error Surface

​ 我刚才举的那些数字,不是真正的例子,以下的数字,是真实的例子,是这个频道真实的后台的数据,所计算出来的结果,那我们可以调整不同的w,我们可以调整不同的b,求取各种w 求取各种b,组合起来以后,我们可以為不同的w跟b的组合,都去计算它的Loss,然后就可以画出以下这一个等高线图.

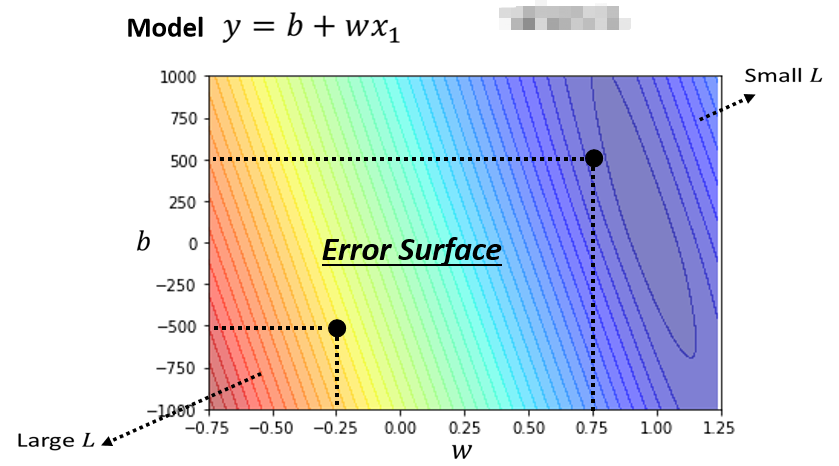
​ 在这个等高线图上面,越偏红色系,代表计算出来的Loss越大,就代表这一组w跟b越差,如果越偏蓝色系,就代表Loss越小,就代表这一组w跟b越好,拿这一组w跟b,放到我们的Function裡面,放到我们的Model裡面,那我们的预测会越精準,所以你就知道说,假设w在负0.25,这个b在负500,就代表说呢这个W在负0.25,b在负500 就代表说,这个频道每天看的人越来越少,而且Loss这麼大,跟真实的状况不太合,如果w代0.75 b代500,那这个正确率,这个估测会比较精準,那估测最精準的地方看起来,应该是在这裡啦,如果你今天w代一个很接近1的值,b带一个小小的值,比如说100多,那这个时候估测是最精準的,那这跟大家的预期可能是比较接近的,就是你拿前一天的点阅的总次数,去预测隔天的点阅的总次数,那可能前一天跟隔天的点阅的总次数,其实是差不多的,所以w设1,然后b设一个小一点的数值,也许你的估测就会蛮精準的,那像这样子的一个等高线图,就是你试著试了不同的参数,然后计算它的Loss,画出来的这个等高线图,叫做==Error Surface==,那这个是机器学习的第二步,

3. Optimization

​ 接下来我们进入机器学习的第三步,那第三步要做的事情,其实是==解一个最佳化的问题==,如果你不知道最佳化的问题,是什麼的话也没有关係,我们今天要做的事情就是,找一个w跟b,把未知的参数,找一个数值出来,看代那一个数值进去,可以让我们的大L,让我们的Loss的值最小,那个就是我们要找的w跟b,那这个可以让loss最小的w跟b,我们就叫做$w\ast$ 跟 $b\ast ,$代表说他们是最好的一组w跟b,可以让loss的值最小.

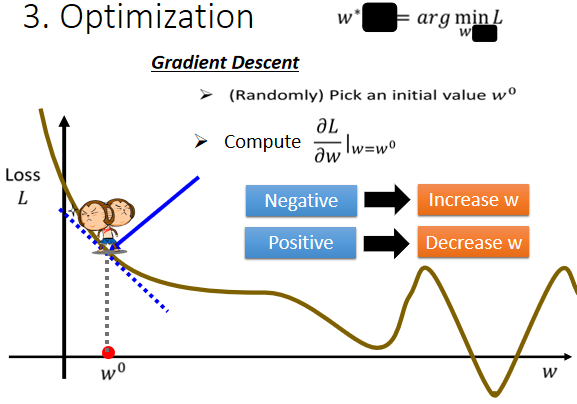
​ 在这一门课裡面 我们唯一会用到的,Optimization的方法,叫做==Gradient Descent==。為了要简化起见,我们先假设我们未知的参数只有一个,就是$w$,我们先假设没有b那个未知的参数,只有w这个未知的参数.

​ 那当我们w代不同的数值的时候,我们就会得到不同的Loss,这一条曲线就是error surface,只是刚才在前一个例子裡面,我们看到的error surface,是二维的是2D的,那这边只有一个参数,所以我们看到的这个error surface,是1D的.

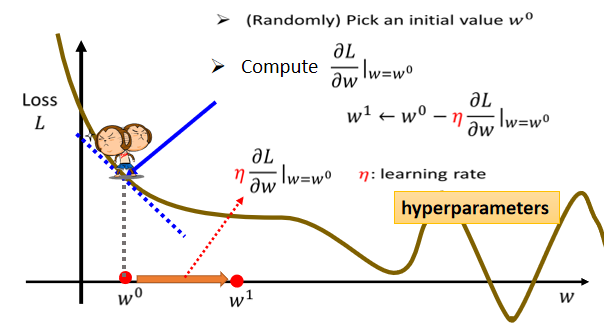
==那怎麼样找一个w,去让这个loss的值最小呢?==

• 那首先你要随机选取一个初始的点,那这个初始的点,我们叫做**$w_0$**,那这个初始的点往往真的就是随机的,那在往后的课程裡面,我们其实会看到也许有一些方法,可以给我们一个比较好的w零的值.我们先当作都是随机的,那假设我们随机决定的结果,是在w0这个地方。

• 那接下来你就要计算,在w等於w0的时候,w这个参数对loss的微分是多少$\partial L/\partial w|(w=w^0)$,如果你不知道微分是什麼的话,那没有关係反正我们做的事情就是,计算在这一个点,在w₀这个位置的error surface的切线斜率,也就是这一条蓝色的虚线,它的斜率,那如果这一条虚线的斜率是负的,那代表什麼意思呢,代表说左边比较高 右边比较低,在这个位置附近,左边比较高 右边比较低。

• 那如果左边比较高右边比较低的话,我们就把w的值变大,那我们就可以让loss变小,如果算出来的斜率是正的,就代表说左边比较低右边比较高,是这个样子的,左边比较低右边比较高,如果左边比较低 右边比较高的话,那就代表我们把w变小了,w往左边移 我们可以让Loss的值变小,那这个时候你就应该把w的值变小,那假设你连斜率是什麼都不知道的话,也没有关係,你就想像说有一个人站在这个地方,然后他左右环视一下,那这一个算微分这件事啊,就是左右环视,它会知道左边比较高还是右边比较高,看哪边比较低,它就往比较低的地方跨出一步,

  那这一步要跨多大呢,这一步的步伐的大小取决於两件事情,

  • 第一件事情是这个地方的斜率有多大,这个地方的斜率大,这个步伐就跨大一点,斜率小步伐就跨小一点,
  • 另外 除了斜率以外,就是除了微分这一项,还有另外一个东西会影响步伐大小,这个东西我们这边用$\eta$来表示,这个$\eta$叫做==learning rate==,叫做学习速率,这个learning rate 它是怎麼来的呢,==它是你自己设定的,你自己决定这个$\eta$的大小==,如果$\eta$设大一点,那你每次参数update就会量大,你的学习可能就比较快,如果η设小一点,那你参数的update就很慢,每次只会改变一点点参数的数值,那这种你在做机器学习,需==要自己设定的东西,叫做hyperparameters==

有同学问说,為什麼loss可以是负的呢?

​ Loss这个函数是自己定义的,所以在刚才我们的定义裡面,我们说loss就是估测的值,跟正确的值,它的绝对值,那如果根据刚才loss的定义,那它不可能是负的,但是loss的这一个function,是你自己决定的,你可以说,我今天要决定一个loss function,就是绝对值再减100,那你可能就有负的,所以我这边这一个curve,我这边可能刚才忘了跟大家说明说,这个curve并不是一个真实的loss,它是我随便乱举的一个例子,因為在今天,我想要举一个比较general 的case,它并不是一个真实任务的,Error surface,所以这个loss的这个curve,这个error surface,它可以是任何形状,这边没有预设立场说,它一定要是什麼形状,但是确实在真实,在刚才这一个如果loss的定义,就跟我刚才定的一样是绝对值,那它就不可能是负值,但这个loss,这个function是你自己决定的,所以它有可能是负的

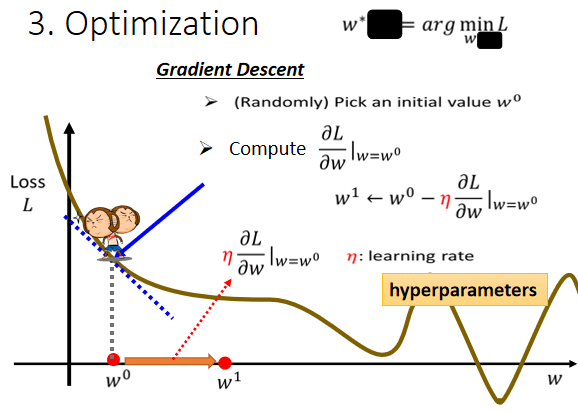
​ 那我们说我们要把w⁰往右移一步,那这个新的位置就叫做w¹,这一步的步伐是η乘上微分的结果,那如果你要用数学式来表示它的话,就是把w⁰减掉η乘上微分的结果,得到w¹

$$w^1\leftarrow w^0-\eta \frac{\partial L}{\partial w}|(w=w^0)$$

,那接下来你就是反覆进行刚才的操作,你就计算一下w¹微分的结果,然后再决定现在要把w¹移动多少,然后再移动到w²,然后你再继续反覆做同样的操作,不断的把w移动位置,最后你会停下来.

==**什麼时候会停下来呢?**往往有两种状况==,

• 第一种状况是你失去耐心了,你一开始会设定说,我今天在调整我的参数的时候,我在计算我的微分的时候,我最多计算几次,你可能会设说,我的上限就是设定100万次,就我参数更新100万次以后,我就不再更新了,那至於==要更新几次,这个也是一个hyperparameter,这个是你自己决定的==,做一个deadline是明天,那你可能更新的次数就设少一点,对它下周更新的次数就设多一点,
• 那还有另外一种理想上的,停下来的可能是,今天当我们不断调整参数,调整到一个地方,它的微分的值就是这一项,算出来正好是0的时候,如果这一项正好算出来是0,0乘上learning rate η还是0,所以你的参数就不会再移动位置,那假设我们是这个理想的状况,我们把w⁰更新到w¹,再更新到w²,最后更新到wᵗ有点卡,wᵗ卡住了,也就是算出来这个微分的值是0了,那参数的位置就不会再更新,

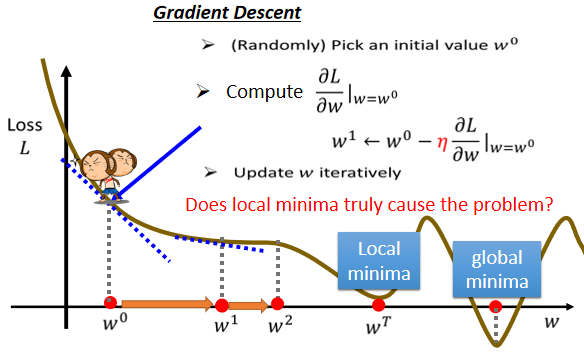
​ 你可能会马上发现说,Gradient Descent 这个方法,有一个巨大的问题,我们没有找到真正最好的解,我们没有找到那个,可以让Loss最小的那个w,在这个例子裡面,把w设定在右侧红点附近这个地方,你可以让loss最小,但是如果 Gradient Descent,是从W^0^这个地方,当作随机初始的位置的话,也很有可能走到W^T^这裡,你的训练就停住了,你就没有办法再移动w的位置。

​ 那右侧红点这一个位置,这个真的可以让loss最小的地方,叫做==global 的minima==,而W^T^这个地方叫做==local 的minima==,它的左右两边,都比这个地方的loss还要高一点,但是它不是整个error surface上面的最低点。

​ 所以常常可能会听到有人讲到,Gradient Descent,不是个好方法,这个方法会有local minima的问题,没有办法真的找到global minima,但教科书常常这样讲,农场文常常这样讲,但这个其实只是幻觉而已,事实上,假设你有做过深度学习相关的事情,假设你有自己训练network,自己做过Gradient Descent 经验的话,其实local minima是一个假问题,我们在做Gradient Descent 的时候,真正面对的难题不是local minima,到底是什麼,这个 我们之后会再讲到,在这边你就先接受,先相信多数人的讲法说,Gradient Descent,有local minima的问题,在这个图上在这个例子裡面,显然有local minima的问题,但之后会再告诉你说,Gradient Descent真正的痛点,到底是什麼。

​ 刚才举的例子,是只有一个参数的例子而已,那实际上我们刚才的模型有两个参数,有w跟b,那有两个参数的情况下,怎麼用Gradient Descent呢,其实跟刚才一个参数没有什麼不同,若一个参数你没有问题的话,你可以很快的推广到两个参数。

• 我们现在有两个参数,都给它随机的初始的值,就是$w^0$跟$b^0$

• 你要计算w跟loss的微分,你要计算b对loss的微分,计算是在w等於w⁰的位置,b等於b₀的位置,在w等於w₀的位置,b等於b⁰的位置,你要计算w对L的微分,计算b对L的微分,

  $$\frac{\partial L}{\partial b}|(w=w^0,b=b^0)$$ $$\frac{\partial L}{\partial w}|(w=w^0,b=b^0)$$

  计算完以后,就根据我们刚才,一个参数的时候的做法,去更新w跟b,把w⁰减掉learning rate,乘上微分的结果得到w¹,把b⁰减掉learning rate,乘上微分的结果得到b¹

  $$w^1\leftarrow w^0-\eta \frac{\partial L}{\partial w}|(w=w^0,b=b^0)$$

$$b^1\leftarrow b^0-\eta \frac{\partial L}{\partial b}|(w=w^0,b=b^0)$$

​ 如果你不会算微分的话,不用紧张,在deep learning 的framework裡面,或在我们作业一,会用的pytorch裡面,算微分都是程式自动帮你算的,你就co一行 就写一行程式,自动就把微分的值就算出来了,你就算完全不知道自己在干嘛,也还是可以把微分的值算出来,所以这边,如果你根本就不知道微分是什麼,不用担心,这一步骤就是一行程式,这个等一下之后在做AE的时候,大家可以自己体验看看,那就是反覆同样的步骤,就不断的更新w跟b,然后期待最后,你可以找到一个最好的w,$w^{\ast }$ 跟最好的b $b^{\ast }$.

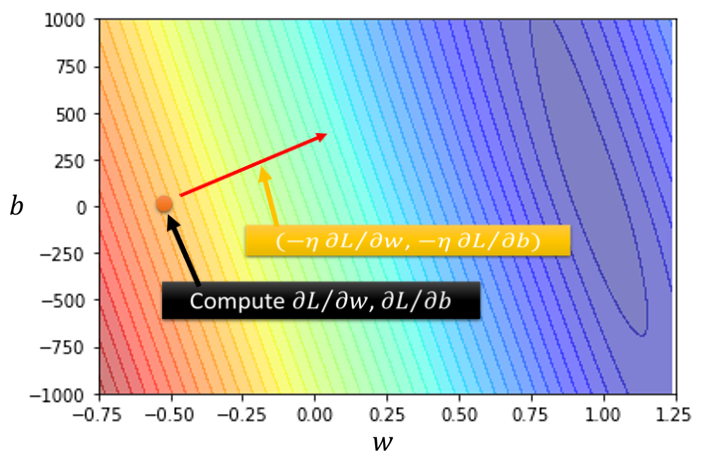
​ 如果在这一个问题上,它操作起来是什麼样子,假设,你随便选一个初始的值在这个地方,那你就先计算一下w对L的微分,跟计算一下b对L的微分,然后接下来你就要更新w跟b,更新的方向就是w对L的微分,乘以η再乘以一个负号,b对L的微分,算出这个微分的值,你就可以决定更新的方向,你就可以决定w要怎麼更新,那把w跟b更新的方向结合起来,就是一个向量,就是这个红色的箭头,我们就从这个位置移到这个位置,

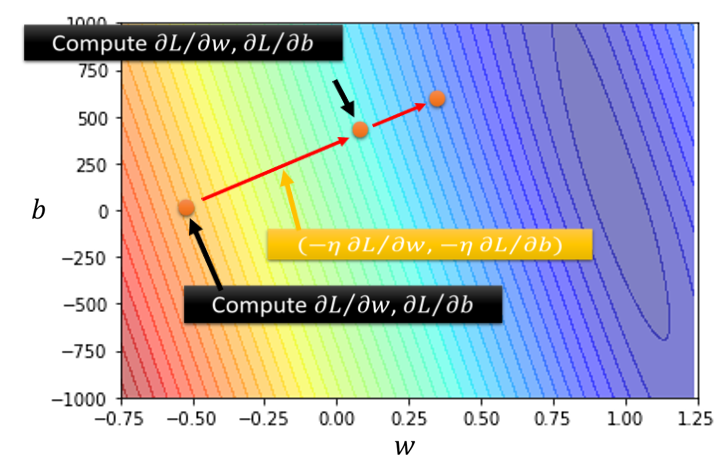
​ 然后再计算一次微分,然后你再决定要走什麼样的方向,把这个微分的值乘上learning rate,再乘上负号,你就知道红色的箭头要指向那裡,你就知道怎麼移动w跟b的位置,一直移动一直移动一直移动,期待最后可以找出一组不错的w跟b,

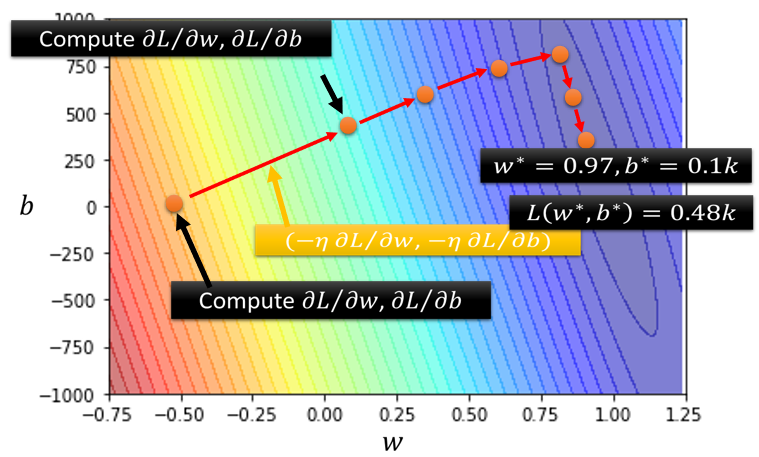
​ 那实际上真的用Gradient Descent,进行一番计算以后,这个是真正的数据,我们算出来的最好的w是0.97,最好的b是0.1k,跟我们的猜测蛮接近的,因為x₁的值可能跟y很接近,所以这个w就设一个接近1的值,b就设一个比较偏小的值,那loss多大呢,loss算一下是0.48k,也就是在2017到2020年的资料上,如果使用这一个函式,b代0.1k,w代0.97,那平均的误差是0.48k,也就是它的预测的观看人数误差,大概是500人次左右.

Linear Model

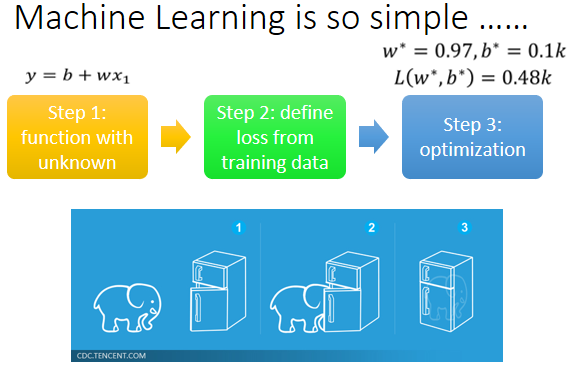
​ 那w跟b的值刚才已经找出来的,那这组w跟b可以让loss小到0.48k,但是这样,是一个让人满意或值得称道的结果吗,也许不是,因為==这三个步骤合起来==,叫做==训练==,我们现在是在,我们已经知道答案的资料上,去计算loss,我们其实已经知道2017到2020年,每天的观看次数 所以,其实我们现在其实只是在自high而已,就是假装我们不知道隔天的观看次数,然后拿这一个函式来进行预测,发现误差是0.48k。

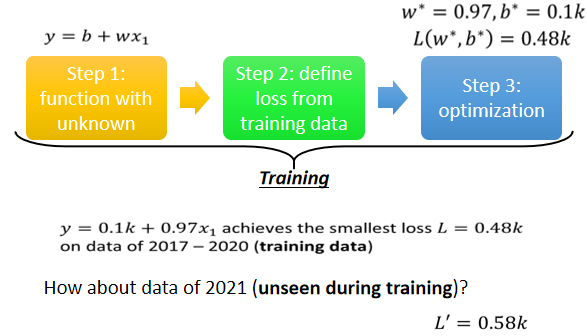
​ 但是我们真正要在意的,我们不知道的,未来的观看的次数是多少,所以我们接下来要做的事情就是拿这个函式,来真的预测一下未来的观看次数,那这边,我们只有2017年到2020年的值,我们在2020年的最后一天,跨年夜的时候,找出了这个函式,接下来从2021年开始每一天,我们都拿这个函式,去预测隔天的观看人次,我们就拿2020年的12月31号的,观看人次,去预测2021年元旦的观看人次,用2021年元旦的观看人次,预测一下2021年元旦隔天,1月2号的观看人次,用1月2号的观看人次去预测,1月3号的观看人次,每天都做这件事,一直做到2月14号,就做到情人节,然后得到平均的值,平均的误差值是多少呢,这个是真实的数据的结果,在2021年没有看过的资料上,这个误差值是,我们这边用L prime来表示,它是0.58,所以在有看过的资料上,在训练资料上,误差值是比较小的,在没有看过的资料上,在2021年的资料上,看起来误差值是比较大的,那我们每一天的平均误差,有580人左右,600人左右。

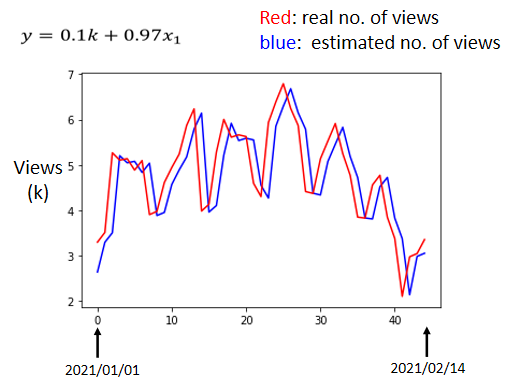
​ 能不能够做得更好呢,在做得更好之前,我们先来分析一下结果

• 横轴是代表的是时间,所以0这个点 最左边的点,代表的是2021年1月1号,最右边点,代表的是2021年2月14号
• 纵轴就是观看的人次,这边是用千人当作单位,
• 红色的线是真实的观看人次
• 蓝色的线是机器用这一个函式,预测出来的观看人次

​ 你有发现很明显的,这蓝色的线没什麼神奇的地方,它几乎就是,红色的线往右平移一天而已,它其实也没做什麼特别厉害的预测,就把红色的线往右平移一天,因為这很合理,因為我们觉得,x₁也就是前一天的观看人次,跟隔天观看人次的,要怎麼拿前一天的观看人次,去预测隔天的观看人次呢,前一天观看人次乘以0.97,加上0.1k 加上100,就是隔天的观看人次,所以你会发现说,机器几乎就是拿前一天的观看人次来预测,隔天的观看人次,但是如果你仔细观察这个图,你就会发现,这个真实的资料有一个很神奇的现象,它是有週期性的,它每隔七天就会有两天特别低,两天观看的人特别少,那两天是什麼日子呢,那我发现那两天都固定,是礼拜五跟礼拜六,礼拜五跟礼拜六我可以了解,就礼拜五週末 大家出去玩,谁还要学机器学习,礼拜六谁还要学机器学习,那不知道為什麼,礼拜天大家去学机器学习,这个我还没有参透為什麼是这个样子,也许跟youtube背后,神奇的演算法有关係,比如说youtube都会推频道的影片,也许youtube在推频道的影片的时候,它都选择礼拜五礼拜六不推,只推礼拜天到礼拜四,可是為什麼推礼拜天到礼拜四呢,这个我也不了解,但是反正看出来的结果,我们看真实的数据,就是这个样子,每隔七天一个循环,每个礼拜五礼拜六,看的人就是特别少。所以既然我们已经知道每隔七天,就是一个循环,那这一个式子 这一个model,显然很烂,因為它只能够看前一天。

​ 每隔七天它一个循环,如果我们一个模型,它是参考前七天的资料,把七天前的资料,直接复製到拿来当作预测的结果,也许预测的会更準也说不定,所以我们就要修改一下我们的模型,通常一个模型的修改,往往来自於你对这个问题的理解,也就是Domain Knowledge。

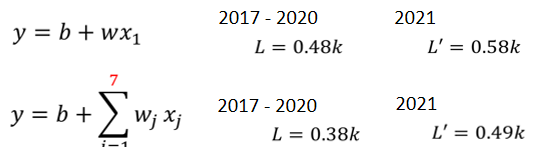
​ 所以一开始,我们对问题完全不理解的时候,我们就胡乱写一个

$$y=b+w{x}_1$$

​ 并没有做得特别好,接下来我们观察了真实的数据以后,得到一个结论是,每隔七天有一个循环,所以我们应该要把,前七天的观看人次都列入考虑,所以我们写了一个新的模型,

​ xⱼ代表什麼,这个下标j代表是几天前,然后这个j等於1到7,也就是从一天前两天前,一直考虑到七天前,那七天前的资料,通通乘上不同的weight,乘上不同的wⱼ,加起来,再加上bias,得到预测的结果,

​ 如果这个是我们的model,那我们得到的结果是怎麼样呢,我们在训练资料上的loss是0.38k,那因為这边只考虑一天,这边考虑七天,所以在训练资料上,你会得到比较低的loss,这边考虑了比较多的资讯,在训练资料上你应该要得到更好的,更低的loss,这边算出来是0.38k,但它在没有看过的资料上面,做不做得好呢,在没有看到的资料上,有比较好,是0.49k,所以刚才只考虑一天是0.58k的误差,考虑七天是0.49k的误差。

​ 那这边每一个w跟b,我们都会用Gradient Descent,算出它的最佳值,它的最佳值长什麼样子呢,这边show出来,给你看 它的最佳值长这样,当然机器的逻辑我是有点没有办法了解,我本来以為它会选七天前的数据,七天前的观看人数,直接复製过来,我看来它没有这样选就是了。

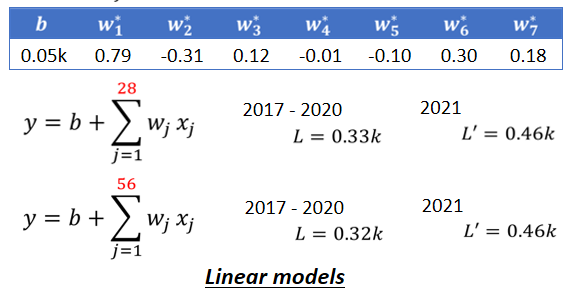
​ 它的逻辑是前一天,跟你要预测的隔天的数值的关係很大,所以w₁*是0.79,那不知道為什麼 它还考虑前三天,前三天是0.12,然后前六天是0.3,前七天是0.18,不过它知道说,如果是前两天前四天前五天,它的值会跟未来我们要预测的,隔天的值是成反比的,所以w₂ w₄跟w₅它们最佳的值,让Loss可以在训练资料上,是0.38k的值 是负的,但是w₁ w₃ w₆跟w₇是正的,我们考虑前七天的值,那你可能会问说,能不能够考虑更多天呢,可以,那这个轻易的改考虑更多天,本来是考虑前七天

​ 然后考虑28天会怎麼样呢,28天就一个月,考虑前一个月每一天的观看人次,去预测隔天的观看人次,预测出来结果怎样呢,训练资料上是0.33k,那在2021年的资料上,在没有看过的资料上是0.46k,看起来又更好一点 好 28天,好那接下来考虑56天会怎麼样呢,在训练资料上是稍微再好一点,是0.32k,在没看过的资料上还是0.46k,看起来,考虑更多天没有办法再更进步了,看来考虑天数这件事,也许已经到了一个极限,好那这边这些模型,它们都是把输入的这个x,这个x 还记得它叫什麼吗,它叫做feature,把feature乘上一个weight,再加上一个bias就得到预测的结果,这样的模型有一个共同的名字,叫做==Linear model==,那我们接下来会看,怎麼把Linear model做得更好。