13 | 魔数 0x5f3759df

你好，我是陈皓，网名左耳朵耗子。

下列代码是在《雷神之锤III竞技场》源代码中的一个函数（已经剥离了C语言预处理器的指令）。其实，最早在2002年（或2003年）时，这段平方根倒数速算法的代码就已经出现在Usenet与其他论坛上了，并且也在程序员圈子里引起了热烈的讨论。

我先把这段代码贴出来，具体如下：

float Q_rsqrt( float number )
{
    long i;
    float x2, y;
    const float threehalfs = 1.5F;

    x2 = number * 0.5F;
    y  = number;
    i  = * ( long * ) &y; // evil floating point bit level hacking
    i  = 0x5f3759df - ( i >> 1 );  // what the fuck?
    y  = * ( float * ) &i;
    y  = y * ( threehalfs - ( x2 * y * y ) );  // 1st iteration
    // 2nd iteration, this can be removed
    // y  = y * ( threehalfs - ( x2 * y * y ) );

    return y;
}

这段代码初读起来，我是完全不知所云，尤其是那个魔数0x5f3759df，根本不知道它是什么意思，所以，注释里也是 What the fuck。今天这节课，我主要就是想带你来了解一下这个函数中的代码究竟是怎样出来的。

其实，这个函数的作用是求平方根倒数，即 $x^{-1/2}$ ，也就是下面这个算式：

$\\frac{1}{\\sqrt{x}}$

当然，它算的是近似值。只不过这个近似值的精度很高，而且计算成本比传统的浮点数运算平方根的算法低太多。在以前那个计算资源还不充分的年代，在一些3D游戏场景的计算机图形学中，要求取照明和投影的光照与反射效果，就经常需要计算平方根倒数，而且是大量的计算——对一个曲面上很多的点做平方根倒数的计算。也就是需要用到下面的这个算式，其中的x,y,z是3D坐标上的一个点的三个坐标值。

$\\frac{1}{\\sqrt{x^{2}+y^{2}+z^{2}}}$

基本上来说，在一个3D游戏中，我们每秒钟都需要做上百万次平方根倒数运算。而在计算硬件还不成熟的时代，这些计算都需要软件来完成，计算速度非常慢。

我们要知道，在上世纪90年代，多数浮点数操作的速度更是远远滞后于整数操作。所以，这段代码所带来的作用是非常大的。

计算机的浮点数表示

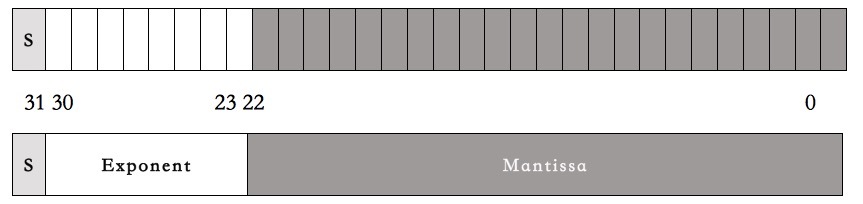
为了讲清楚这段代码，我们需要先了解一下计算机的浮点数表示法。在C语言中，计算机的浮点数表示用的是IEEE 754 标准，这个标准的表现形式其实就是把一个32bits分成三段。

第一段占1bit，表示符号位。代称为S（sign）。
第二段占8bits，表示指数。代称为E（Exponent）。
第三段占23bits，表示尾数。代称为M（Mantissa）。

如下图所示：

然后呢，一个小数的计算方式是下面这个算式：

$(-1)^{S}\\ast(1+\\frac{M}{2^{23}})\\ast 2^{(E-127)}$

但是，这个算式基本上来说，完全就是让人一头雾水，摸不着门路。对于浮点数的解释基本上就是下面这张漫画里表现的样子。

下面，让我来试着解释一下浮点数的那三段表示什么意思。

第一段符号位。对于这一段，我相信应该没有人不能理解。
第二段指数位。什么叫指数？也就是说，对于任何数x，其都可以找到一个 $n$ ，使得 $2^{n}$ <=x<= $2^{n+1}$ 。比如：对于3来说，因为 2 < 3 < 4，所以 n=1。而浮点数的这个指数为了要表示0.00x的小数，所以需要有负数，这8个bits本来可以表示0-255。为了表示负的，取值要放在 [-127,128] 这个区间中。这就是为什么我们在上面的公式中看到的 $2^{(E-127)}$ 这一项了。也就是说， $n = E-127$ ，如果 $n=1$ ，那么 $E$ 就是128了。
第三段尾数位。也就是小数位，但是这里叫偏移量可能好一些。这里的取值是在[ 0 - $2^{23}$ ]中。你可以认为，我们把一条线分成 $2^{23}$ 个线段，也就是8388608个线段。也就是说，把 $2^{n}$ 到 $2^{n+1}$ 分成了8388608个线段。而存储的M值，就是从 $2^n$ 到 x 要经过多少个段。这要计算一下， $2^{n}$ 到x的长度占 $2^{n}$ 到 $2^{n+1}$ 长度的比例是多少。

我估计你对第三段还是有点不懂，那么我们来举一个例子。比如说，对3.14这个小数。

是正数。所以，S = 0。
$2^1$ < 3.14 < $2^2$ 。所以，n=1， n+127 = 128。所以，E=128。
(3.14 - 2) / (4 - 2) = 0.57，而 $0.57\*2^{23} = 4781506.56$ ，四舍五入，得到M = 4781507。因为有四舍五入，所以，产生了浮点数据的精度问题。

把S、E、M转成二进制，得到 3.14的二进制表示。

我们再用IEEE 754的那个算式来算一下：

${(-1)}^0\*({1+\\frac{4781507}{2^{23}}})\*2^{(128-127)}$

$=1\*(1+0.5700000524520874)\*2$

$=3.1400001049041748046875$

你看，浮点数的精度问题出现了。

我们再来看一个示例，小数 0.015。

是正数。所以，S = 0。
$2^{-7}< 0.015 < 2^{-6}$ 。所以，n=-7， n+127 = 120。所以，E=120。
$(0.015 - 2^{-7}) / (2^{-6} - 2^{-7})$ = $0.0071875/0.0078125=0.92$ 。而 $0.92 \* 2^{23} = 7717519.36$ ，四舍五入，得到 M = 7717519。

于是，我们得到0.015的二进制编码：

其中：

120 的二进制是01111000
7717519的二进制是11101011100001010001111

返回过来算一下：

$(-1)^{0}\\ast (1+\\frac{7717519}{2^{23}})\\ast 2^{(120-127)}$

$=(1+0.919999957084656)\*0.0078125$

$=0.014999999664724$

你看，浮点数的精度问题又出现了。

我们来用C语言验证一下：

int main() {
    float x = 3.14;
    float y = 0.015;
    return 0;
}

在我的Mac上用lldb 工具 Debug 一下。

(lldb) frame variable
(float) x = 3.1400001
(float) y = 0.0149999997

(lldb) frame variable -f b
(float) x = 0b01000000010010001111010111000011
(float) y = 0b00111100011101011100001010001111

从结果上，完全验证了我们的方法。

好了，不知道你看懂了没有？我相信你应该看懂了。

简化浮点数公式

因为那个浮点数表示的公式有点复杂，我们简化一下：

$(-1)^{S}\\ast (1+\\frac{M}{2^{23}})\\ast 2^{(E-127)}$

我们令， $m = (\\frac{M}{2^{23}} )$ ， $e = (E-127)$ 。因为符号位在 $y= x^{-\\frac{1}{2}}$ 的两端都是0（正数），也就可以去掉，所以浮点数的算式简化为：

$(1+m)\\ast2^{e}$

上面这个算式是从一个32bits二进制计算出一个浮点数。这个32bits的整型算式是：

$M+E\\ast2^{23}$

比如，0.015的32bits的二进制是：00111100011101011100001010001111，也就是整型的：

$7717519+120\\ast 2^{23}$

$= 1014350479$

$= 0X3C75C28F$

平方根倒数公式推导

下面，你会看到好多数学公式，但是请你不要怕，因为这些数学公式只需要高中数学就能看懂的。

我们来看一下，平方根数据公式：

$y=\\frac{1}{\\sqrt\[2\]{x}}=x^{-\\frac{1}{2}}$

等式两边取以2为基数的对数，就有了：

$\\log\_2(y) =-\\frac{1}{2}\\log\_2(x)$

因为我们实际上在算浮点数，所以将公式中的 x 和 y 分别用浮点数的那个浮点数的简化算式 $(1+ m)\*2^e$ 替换掉。代入 $\\log()$ 公式中，我们也就有了下面的公式：

$\\log\_{2} (1+m\_y)+e\_y$

$=-\\frac{1}{2}(\\log\_2(1+m\_x)+e\_x)$

因为有对数，这公式看着就很麻烦，似乎不能再简化了。但是，我们知道，所谓的 $m\_x$ 或是 $m\_y$ ，其实是个在0和1区间内的小数。在这种情况下， $\\log\_2 (1.x)$ 接近一条直线。

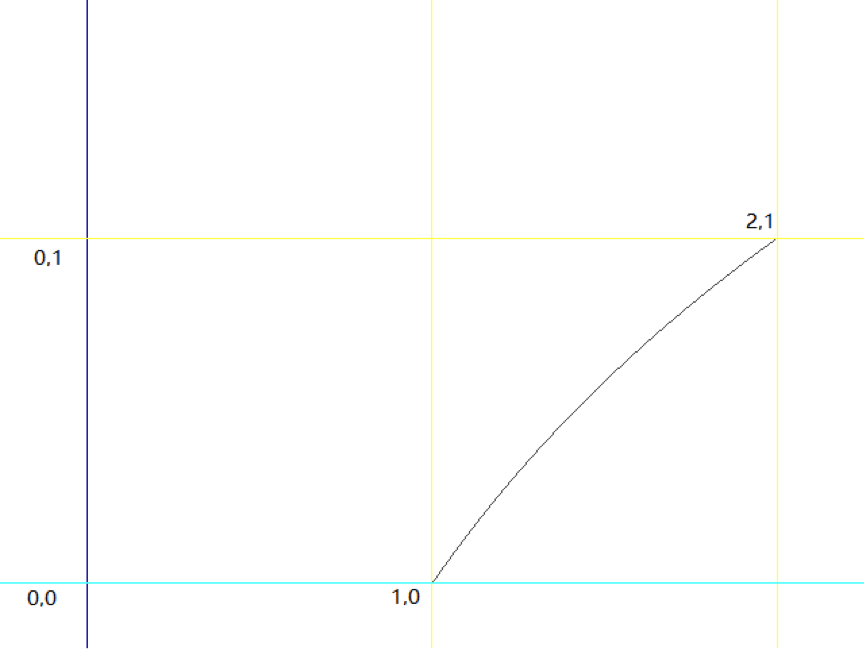
那么我们就可以使用一个直线方程来代替，也就是：

$\\log\_{2}(1+m)\\approx m+\\sigma$

于是，我们的公式就简化成了：

$m\_y+\\sigma+e\_y\\approx-\\frac{1}{2}(m\_x+\\sigma+e\_x)$

因为 $m = (\\frac{M}{2^{23}})$ ， $e = (E-127)$ ，代入公式，得到：

$\\frac{M\_y}{2^{23}}+\\sigma+E\_y-127$

$\\approx-\\frac{1}{2}(\\frac{M\_x}{2^{23}}+\\sigma+E\_x-127)$

移项整理一下，把 σ 和127 从左边，移到右边：

$\\frac{M\_y}{2^{23}}+E\_y\\approx-\\frac{1}{2}(\\frac{M\_x}{2^{23}}+E\_x)-\\frac{3}{2}(\\sigma-127)$

再把整个表达式乘以 $2^{23}$ ，得到：

${M\_y}+E\_y{2^{23}}$

$\\approx-\\frac{1}{2}(M\_x+E\_x{2^{23}})-\\frac{3}{2}(\\sigma-127){2^{23}}$

可以看到一个常数： $-\\frac{3}{2}(\\sigma-127){2^{23}}$ ，把负号放进括号里，变成 $\\frac{3}{2}(127-\\sigma){2^{23}}$ ，并可以用一个常量代数R来取代，于是得到公式：

${M\_y}+E\_y{2^{23}}\\approx R-\\frac{1}{2}(M\_x+E\_x{2^{23}})$

还记得我们前面那个“浮点数32bits二进制整型算式” $M+E\* 2^{23}$ 吗？假设，浮点数x的32bits的整型公式是： $I\_x= M\_x+ E\_x 2^{23}$ ，那么上面的公式就可以写成：

$I\_y\\approx R-\\frac{1}{2}I\_x$

代码分析

让我们回到文章的主题，那个平方根函数的代码。

首先是：

i  = * ( long * ) &y; // evil floating point bit level hacking

这行代码就是把一个浮点数的32bits的二进制转成整型。也就是，前面我们例子里说过的，3.14的32bits的二进制是：01000000010010001111010111000011，整型是：1078523331。即y = 3.14，i = 1078523331。

然后是：

i  = 0x5f3759df - ( i >> 1 );  // what the fuck?

这就是：

i  = 0x5f3759df - ( i / 2 );

也就是我们上面推导出来的那个公式：

$I\_y\\approx R-\\frac{1}{2}I\_x$

代码里的 R = 0x5f3759df。

我们又知道，R = $\\frac{3}{2}(127-\\sigma){2^{23}}$ ，把代码中的那个魔数代入，就可以计算出来：σ= 0.0450465 。这个数是个神奇的数字，这个数是怎么算出来的，现在还没人知道。不过，我们先往下看后面的代码：

    x2 = number * 0.5F;
    y  = * ( float * ) &i;
    y  = y * ( threehalfs - ( x2 * y * y ) );  // 1st iteration
    // 2nd iteration, this can be removed
    // y  = y * ( threehalfs - ( x2 * y * y ) );

这段代码相当于下面这个公式：

$I\_{y’} = I\_y(1.5-0.5 x I\_y^2)$

这个其实是“牛顿求根法”，这是一个为了找到一个 f(x)= 0 的根而用一种不断逼近的计算方式。请看下图：

首先，初始值为X0，然后找到X0所对应的Y0（把X0代入公式得到Y0 = f(X0)），然后在（X0,Y0）这个点上做一个切线，得到与X轴交汇的X1。再用X1做一次上述的迭代，得到X2，就这样一直迭代下去，一直找到，y = 0时，x的值。

牛顿法的通用公式是：

$x\_{n+1}=x\_n-\\frac{f(x\_n)}{f’(x\_n)}$

于是，对于 $y= \\frac{1}{\\sqrt{x}}$ 来说，对固定的x（常数），我们求y使得 $\\frac{1}{y^2}-x=0$ ， $f(y)= \\frac{1}{y^2} -x$ , $f’(y)=\\frac{-2}{y^3}$ 。注意： $f’(y)$ 是 $f(y)$ 关于y的导数。

代入上述的牛顿法的通用公式后得到：

$y\_{n+1}=y\_n-\\frac{\\frac{1}{y\_n^2}-x}{\\frac{-2}{y\_n^3}}$

$=\\frac{y\_n(3-xy\_n^2)}{2}=y\_n(1.5-0.5xy\_n^2)$

正好就是我们上面的代码。

整个代码是，之前生成的整数操作产生首次近似值后，将首次近似值作为参数送入函数最后两句进行精化处理。代码中的两次迭代正是为了进一步提高结果的精度。但由于《雷神之锤III》的图形计算中并不需要太高的精度，所以代码中只进行了一次迭代，二次迭代的代码则被注释了。

计算机的浮点数表示

简化浮点数公式

平方根倒数公式推导

代码分析

相关历史