工程矩阵的定义
分块矩阵
分块矩阵的乘法可以表示为:
A B = ( A 11 A 21 A 12 A 22 ) ( B 11 B 21 B 12 B 22 )
对于分块矩阵,有性质:( A B ) ∗ = ( A ∗ , B ∗ )
矩阵方程组
设方程组 A x = b A = ( a ij ) m × n b = ( b i ) m × 1
有解 ⇔ r ( A ) = r ( A , b )
若 r ( A ) = r ( A , b ) = r < n n − r
若 r ( A ) = r ( A , b ) = r = n
齐次线性方程组的基础解系
对齐次线性方程组 A x = 0 , A = ( a ij ) m × n
非零解 ⇔ r ( A ) < n
若 r ( A ) = r < n n − r
若 r ( A ) = r < n n − r
高斯消元法 :
用初等行变换将 A
确定自由未知量
用回代法找出通解
极大无关组
设向量组 α 1 , α 2 , ⋯ , α m α i 1 , α i 2 , ⋯ , α i r
α i 1 , α i 2 , ⋯ α 1 , α 2 , ⋯ , α m α i 1 , α i 2 , ⋯ , α i r
则称 α i 1 , α i 2 , ⋯ , α i r α 1 , ⋯ , α m
定理 :
若向量组的秩�为 r r
如果一向量组的极大无关组中含 r r
矩阵的等价标准形
s × n A r ⇒ P s × s , Q n × n A = P ( I r 0 0 0 ) Q
消去分解
s × n A r s × r B r × n C A = BC
定理 :
r ( A + B ) ≤ r ( A ) + r ( B ) r ( A B ) ≤ r ( A ) , r ( B ) r ( A ) + r ( B ) ≤ r ( ( A kk , B kk ) ) + n
线性空间和线性变换
线性空间的定义和性质
线性空间的定义
线性空间满足下述三个要求建立的八条公理:
一个数域 K V
两个运算:
加法:∀ x , y ∈ V x + y ∈ V
数乘运算:∀ a ∈ K , x ∈ V a x ∈ V
这两个运算满足如下八条公理:
加法交换律:∀ α , β ∈ V , α + β = β + α
加法结合律:∀ α , β , γ ∈ V , ( α + β ) + γ = α + ( β + γ )
零元存在性:存在 0 ∈ V ∀ α ∈ V α + 0 = α
负元存在性:∀ α ∈ V β ∈ V α + β = 0
数乘结合律:∀ λ ∈ K , α ∈ V , λ α ∈ V
乘法结合律:∀ k 1 , k 2 ∈ K , ∀ α ∈ V k 1 ( k 2 α ) = ( k 1 k 2 ) α
分配律一:∀ k ∈ F , ∀ α , β ∈ V k ( α + β ) = k α + k β
分配律二:�∀ k 1 , k 2 ∈ F , ∀ α ∈ V ( k 1 + k 2 ) α = k 1 α + k 2 α
线性空间的性质
设 V 是数域 F 上的线性空间,∀ α , β , γ ∈ V , k ∈ K
V 中的零元是唯一的,通常记为 0
任何一个向量的负向量是唯一的,通常记为 − a
加法满足消去律:若 α + γ = β + γ α = β
若 α + β = 0 α = − β β = − α
k ⋅ 0 = 0 0 ⋅ α = 0 ( − k ) α = − k α ( − 1 ) α = − α
线性相关与线性无关
定义
设 α 1 , α 2 , ⋯ , α n ∈ V k 1 , k 2 , ⋯ , k n k 1 α 1 + k 2 α 2 + ⋯ + k n α n = 0 α 1 , α 2 , ⋯ , α n
性质
若 n ≥ 2 α 1 , α 2 , ⋯ , α n α i
向量 α 1 , α 2 , ⋯ , α n α 1 , α 2 , ⋯ , α n , α n + 1 α n + 1
推论
若 β 1 , β 2 , ⋯ , β n α 1 , α 2 , ⋯ , α n β 1 , ⋯ , β n α 1 , ⋯ , α n
若 β 1 , β 2 , ⋯ , β n α 1 , α 2 , ⋯ , α n α i = β i
基和维数
基的定义
若 α 1 , α 2 , ⋯ , α n ∈ V
向量组 α 1 , ⋯ , α n
∀ β ∈ V α 1 , ⋯ , α n α 1 , ⋯ , α n 基
基的性质
线性空间的基不一定存在,仅当一个空间由有限向量系生成 ,基相当于可以简明生成 的最简集
注意 :有限维线性空间 V
维数
若 V 的某一组基中含 n 个向量,则 V 的任一组基中都含 n 个向量
称 V 是 n 维空间,记为 dim V = n
规定零空间的维数为 0
维数的性质
若 dim V = n n + 1
定理 :若 dim V = n n
坐标和形式记导
坐标的定义
设 α 1 , α 2 , ⋯ , α n β ∈ V β = x 1 α 1 + x 2 α 2 + ⋯ + x n α n ( x 1 , x 2 , ⋯ , x n ) β α 1 , ⋯ , α n
坐标的性质
假设 η i ∈ V α 1 , ⋯ , α n X i i = 1 , 2 , ⋯ , n
n = 0 ⇒ X = 0 若 η 1 = x 1 α 1 + ⋯ + x n α n X = ( x 1 , x 2 , ⋯ , x n ) T
η 1 , ⋯ , η n ⇔ X 1 , ⋯ , X n
形式记导
X = x 1 x 2 x 3 α 1 , α 2 , α 3 则可形��式记成 β = ( α 1 , α 2 , α 3 ) X
形式记导的性质
若 β i = ( α 1 , α 2 , ⋯ , α n ) A β 1 , β 2 , ⋯ , β n ⇔ A
若有 ( β 1 , β 2 , ⋯ , β n ) = ( α 1 , α 2 , ⋯ , α n ) A ( η 1 , η 2 , ⋯ , η n ) = ( β 1 , β 2 , ⋯ , β n ) B ( η 1 , η 2 , ⋯ , η n ) = ( α 1 , α 2 , ⋯ , α n ) ( A B )
过渡矩阵
定义
设 α 1 , ⋯ , α n β 1 , ⋯ , β n V ( β 1 , ⋯ , β n ) = ( α 1 , ⋯ , α n ) A α 1 , ⋯ , α n β 1 , ⋯ , β n A
性质
过渡矩阵一定是可逆的
由 β 1 , ⋯ , β n α 1 , ⋯ , α n A − 1
若 β 1 , ⋯ , β n γ 1 , ⋯ , γ n B α 1 , ⋯ , α n γ 1 , ⋯ , γ n A B
变换公式
设 X η α 1 , ⋯ , α n Y β 1 , ⋯ , β n ( β 1 , ⋯ , β n ) = ( α 1 , ⋯ , α n ) P Y = PX
子空间
定义
设 V F W V W V F W V W ≤ V
性质
子空间与 V
定理 :设 W ⊆ V W V ⇔ W
解空间
定义
设 A ∈ F m × n V = { η ∈ F n ∣ A η = 0 } A η = 0
性质
生成的子空间
定义
设 V F α 1 , ⋯ , α n ∈ V W = { ∑ k i α i ∣ k i ∈ F } α 1 , ⋯ , α n W = L ( α 1 , ⋯ , α n )
性质
W = L ( α 1 , ⋯ , α n ) V L ( α 1 , ⋯ , α n ) α 1 , ⋯ , α n dim L ( α 1 , ⋯ , α n ) = r ( α 1 , ⋯ , α n ) L ( α 1 , ⋯ , α n ) = L ( β 1 , ⋯ , β n ) ⇔ α 1 , ⋯ , α n β 1 , ⋯ , β n
子空间的运算
子空间的交
定义:V 1 ∩ V 2 = { η ∈ V ∣ η ∈ V 1 , η ∈ V 2 }
性质:V 1 ∩ V 2 V
子空间的和
定义:V 1 + V 2 = { η ∈ V ∣ ∃ η 1 ∈ V 1 , η 2 ∈ V 2 , η = η 1 + η 2 }
性质:
V 1 + V 2 V 定理 :若 V 1 = L ( α 1 , ⋯ , α s ) V 2 = L ( β 1 , ⋯ , β t ) V 1 + V 2 = L ( α 1 , ⋯ , α s , β 1 , ⋯ , β t ) 维数公式 :dim ( V 1 + V 2 ) = dim V 1 + dim V 2 − dim ( V 1 ∩ V 2 )
定义
设 V 1 , V 2 ≤ V ∀ η ∈ V 1 + V 2 η 1 ∈ V 1 , η 2 ∈ V 2 η = η 1 + η 2 V 1 + V 2 V V 1 ⊕ V 2
定理
若 V 1 , V 2 ≤ V
V 1 + V 2 0 V 1 ∩ V 2 = { 0 } dim ( V 1 + V 2 ) = dim V 1 + dim V 2 V 1 , V 2 V 1 + V 2
多个空间的直和
定义
设 V 1 , V 2 , ⋯ , V s ≤ V ∀ η ∈ V 1 + V 2 + ⋯ + V s η i ∈ V i η = ∑ i = 1 s η i V 1 ⊕ V 2 ⊕ ⋯ ⊕ V s V
定理
若 V 1 , V 2 , ⋯ , V s ≤ V
V 1 + V 2 + ⋯ + V s 0 V i ∩ ( ∑ j = i V j ) = { 0 } dim ( ∑ i = 1 s V i ) = ∑ i = 1 s dim V i V 1 , V 2 , ⋯ , V s V 1 + ⋯ + V s
映射相关概念
映射、象、值域
设 f : A → B A , B f a ∈ A f ( a ) B
f f ( A ) = { f ( a ) ∣ a ∈ A } 若 f ( x ) = y y x x y
B f ( A ) f
恒等变换
集合 S I : S → S ; x ↦ x S
单射、满射、双射
设映射 f : S → T
若 f ( S ) = T f
若由 f ( a ) = f ( b ) a = b f
若 f f
定理 :f : S → T ⇔ f
线性映射
定义
设 V , U F f : V → U
∀ v ∈ V , k ∈ F , f ( k v ) = k f ( v ) ∀ x , y ∈ V , f ( x + y ) = f ( x ) + f ( y ) f V U
性质
f ( 0 ) = 0 若 α 1 , … , α n ∈ V , k 1 , … , k n ∈ F f ( ∑ i = 1 n k i α i ) = ∑ i = 1 n k i f ( α i )
若 α 1 , … , α n ∈ V f ( α 1 ) , … , f ( α n ) ∈ U
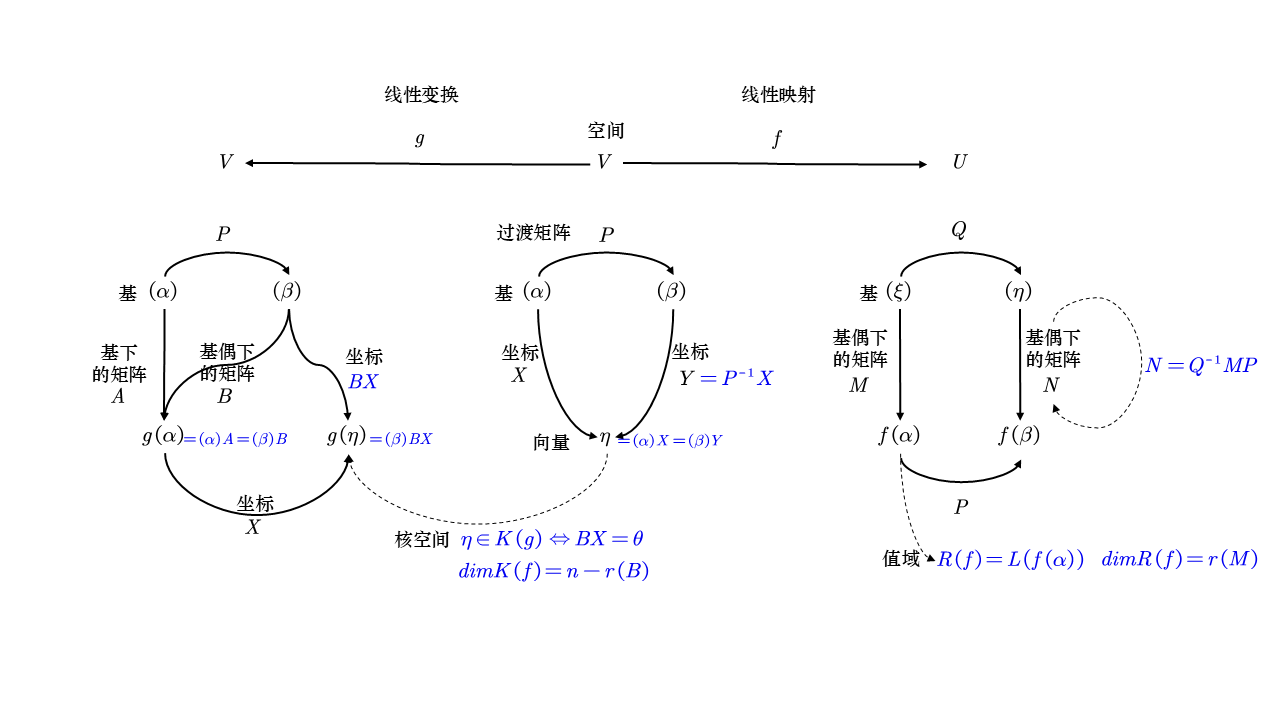
线性变换的运算
设 f , f ′ ∈ Hom ( V , U ) , g ∈ Hom ( U , W ) , k ∈ F k f , f + f ′ , g f
k f : V → U ( k f ) ( x ) = k f ( x ) f + f ′ : V → U ( f + f ′ ) ( x ) = f ( x ) + f ′ ( x ) g f : V → W ( g f ) ( x ) = g ( f ( x )) k f , f + f ′ , g f
值域和核空间
值域
若 V = L ( α 1 , … , α s ) f R ( f ) = { f ( v ) ∣ v ∈ V } = L ( f ( α 1 ) , … , f ( α s ))
定理 :设 f ∈ Hom ( V , U ) f ⇔ R ( f ) = U 定理 :若 f ∈ Hom ( V , U ) V : α 1 , … , α n U : β 1 , … , β s A ( f ( α 1 ) , f ( α 2 ) , ⋯ , f ( α n )) = ( β 1 , β 2 , ⋯ , β s ) A R ( f ) = L ( f ( α 1 ) , … , f ( α n )) f ( α 1 ) , … , f ( α n ) R ( f ) dim R ( f ) = r ( A )
核空间
定义:K ( f ) = { v ∈ V ∣ f ( v ) = 0 } V f
定理 :设 f ∈ Hom ( V , U ) f ⇔ K ( f ) = { 0 } 定理 :若 f ∈ Hom ( V , U ) V : α 1 , … , α n U : β 1 , … , β s A η ∈ V α 1 , … , α n X f ( η ) β 1 , … , β s A X η ∈ K ( f ) ⇔ A X = 0 维数定理 :设 dim V < ∞ , f ∈ Hom ( V , U ) dim R ( f ) + dim K ( f ) = dim V 推论 :设 dim V < ∞ , f ∈ Hom ( V , V ) f ⇔ f ⇔ f
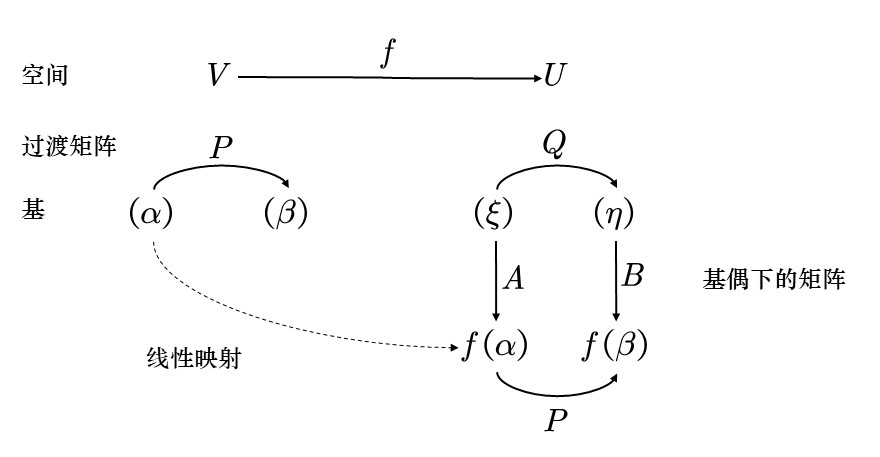
基下的矩阵
定义
设 f ∈ Hom ( V , U ) V : α 1 , … , α n U : β 1 , … , β s ( f ( α 1 ) , f ( α 2 ) , … , f ( α n )) = ( β 1 , β 2 , … , β s ) A A f 特别如果 U = V α i = β i A f
定理
若 f ∈ Hom ( V , U ) V : α 1 , … , α n U : β 1 , … , β s A η ∈ V α 1 , … , α n X f ( η ) β 1 , … , β s A X
设 f ∈ Hom ( V , U ) V : α 1 , … , α n U : β 1 , … , β s A V : α 1 ′ , … , α n ′ U : β 1 ′ , … , β m ′ B α α ′ P β β ′ Q B = Q − 1 A P
设 f ∈ Hom ( V , V ) α 1 , … , α n A α 1 ′ , … , α n ′ B α α ′ P B = P − 1 A P
设 f , g ∈ Hom ( V , V ) V α 1 , … , α n A , B k ∈ F
k f k A f + g A + B f g A B f ⇔ A f − 1 A − 1
不变子空间
定义
设 f ∈ Hom ( V , V ) , W ⊆ V ∀ η ∈ W f ( η ) ∈ W W f
性质
设 f ∈ Hom ( V , V ) R ( f ) , K ( f ) f
W f f ∥ W W 如果 V = V 1 ⊕ V 2 V 1 , V 2 f V 1 α 1 , … , α s V 2 α s + 1 , … , α n α 1 , … , α s , α s + 1 , … , α n V f ( A O O B )
定理 :线性变换在不同的基下的矩阵是相似的
定义
设 U , V F f ∈ Hom ( V , U ) f U , V
如果 U , V U , V V ≅ U
定理
设 f : V → U U , V α 1 , α 2 , … , α s ∈ V α 1 , α 2 , … , α s f ( α 1 ) , f ( α 2 ) , … , f ( α s ) ∈ U
设 U , V F V ≅ U dim V = dim U
内积空间和等距变换
内积的定义与性质
内积的定义
设 V F V ⟨ α , β ⟩
共轭对称性:⟨ α , β ⟩ = ⟨ β , α ⟩
可加性:∀ α , β , γ ∈ V ⟨ α + β , γ ⟩ = ⟨ α , γ ⟩ + ⟨ β , γ ⟩
齐次性:∀ α , β ∈ V , k ∈ F ⟨ k α , β ⟩ = k ⟨ α , β ⟩
正定性:∀ α ∈ V , ⟨ α , α ⟩ ≥ 0 α = 0
则称 ⟨ α , β ⟩ α , β
内积的性质
⟨ α , β + γ ⟩ = ⟨ α , β ⟩ + ⟨ α , γ ⟩ ⟨ α , k β ⟩ = k ⟨ α , β ⟩ ⟨ ∑ i = 1 s k i α i , ∑ j = 1 t l j β j ⟩ = ∑ i = 1 s ∑ j = 1 t k i l j ⟨ α i , β j ⟩ 对任意 α ∈ V , ⟨ α , 0 ⟩ = ⟨ 0 , α ⟩ = 0
标准内积
实数域:⟨ α , β ⟩ = β T α = ∑ i = 1 n a i b i
复数域:⟨ α , β ⟩ = β H α = ∑ i = 1 n a i b i
内积空间
定��义
定义了内积的线性空间称为内积空间
当 F = R V
当 F = C V
度量矩阵
设 ϵ 1 , ϵ 2 , … , ϵ n V α , β ∈ V X = ( x 1 , x 2 , … , x n ) T , Y = ( y 1 , y 2 , … , y n ) T
则 ⟨ α , β ⟩ = ∑ i = 1 n ∑ j = 1 n x i y j ⟨ ϵ i , ϵ j ⟩ = X T A Y
其中,A = ((⟨ ϵ i , ϵ j ⟩) ) n × n A V ϵ 1 , ϵ 2 , … , ϵ n
性质 :
若 F = R A = A T
若 F = C A = A H
长度与距离
长度
设 α ∈ V α ∥ α ∥= ⟨ α , α ⟩ ∥ α ∥= 1 α
性质 :
∀ α ∈ V , ∥ α ∥≥ 0 ∥ α ∥= 0 ⇔ α = 0 ∥ k α ∥= ∣ k ∣ ∥ α ∥
重要定理 :
Cauchy-Schwarz不等式:∀ α , β ∈ V , ∣ ⟨ α , β ⟩ ∣ ≤∥ α ∥∥ β ∥
三角不等式:∀ α , β ∈ V , ∥ α + β ∥≤∥ α ∥ + ∥ β ∥
距离
向量 α , β d ⟨ α , β ⟩ =∥ α − β ∥
三角不等式 :∀ α , β , γ ∈ V , d ( α , γ ) ≤ d ( α , β ) + d ( β , γ )
正交性
定义
若向量 α , β α , β α ⊥ β
由两两正交的非零向量组成的向量组称为��正交向量组
由两两正交的单位向量组成的向量组称为标准正交向量组
由正交向量组组成的基称为正交基
由标准正交向量组组成的基称为标准正交基
重要定理
勾股定理:若 α ⊥ β ∥ α + β ∥ 2 =∥ α ∥ 2 + ∥ β ∥ 2
基扩充定理:假设 W V α 1 , α 2 , … , α s W α s + 1 , α s + 2 , … , α n α 1 , α 2 , … , α s , α s + 1 , α s + 2 , … , α n V
Schmidt正交化
若 α 1 , α 2 , … , α s ∈ V
β 1 = α 1 β k = α k − ∑ j = 1 k − 1 ⟨ β j , β j ⟩ ⟨ α k , β j ⟩ β j k = 2 , … , s 单位化:γ i = ∥ β i ∥ 1 β i , i = 1 , 2 , … , s
酉矩阵
定义
若 A H A = I n A
性质
A是酉矩阵 ⇔ A H A = I ⇔ A − 1 = A H ⇔ A C n
若 A , B A − 1 , A B
设 A A A
重要定理
设 α 1 , α 2 , … , α n V ( γ 1 , γ 2 , … , γ n ) = ( �α 1 , α 2 , … , α n ) U γ 1 , γ 2 , … , γ n ⇔ U
正交补空间
定义
若 W 1 , W 2 ≤ V ∀ α 1 ∈ W 1 , α 2 ∈ W 2 α 1 ⊥ α 2 W 1 ⊥ W 2
设 W ≤ V W ⊥ = { α ∈ V ∣ α ⊥ W } W ⊥ V W V
重要定理
设 W = L ( α 1 , α 2 , … , α s ) η ∈ V η ⊥ W ⇔ η ⊥ α j ∀ j
设 V W V V = W ⊕ W ⊥
若 V = W ⊕ U W ⊥ U U = W ⊥
设 A ∈ C s × n f : C n → C s f ( x ) = A x ∀ x ∈ C n f R ( A ) , K ( A ) R ( A ) ⊥ = K ( A H ) K ( A ) ⊥ = R ( A H )
正投影
定义
已知 W ≤ V , α ∈ V η ∈ W d ( α , η ) = min ξ ∈ W d ( α , ξ ) η α W
重要定理
η ∈ W α W η − α ⊥ W 若 α W
设 W V V W
等距变换
定义
V f ∈ Hom ( V , V ) ⟨ f ( α ) , f ( β )⟩ = ⟨ α , β ⟩ ∀ α , β ∈ V f
性质
若 F = R f
若 F = C f
重要定理
设 V f ∈ Hom ( V , V )
f ∥ f ( α ) ∥=∥ α ∥ f ⟨ f ( α ) , f ( β )⟩ = ⟨ α , β ⟩ f f
欧氏空间中的镜像变换
定义
设 V ω ∈ V f : V → V α ↦ α − 2 ⟨ α , ω ⟩ ω f V
性质
α → β ω = ∥ α − β 0 ∥ 1 ( α − β 0 ) = ∥ α − ∥ β ∥ ∥ α ∥ β ∥ 1 ( α − ∥ β ∥ ∥ α ∥ β )
Hermite
Hermite矩阵
定义
设 A ∈ C n × n A H = A ∀ j , i a ij = a ji ∀ i a ii ∈ R A ∈ C n × n A H = − A
性质
实对称矩阵 :
实对称矩阵的特征值都为实数
实对称矩阵的属于不同特征值的特征向量相互正交
存在正交矩阵 Q Q T A Q
Hermite矩阵 :
所有特征值均为实数
不同特征值的特征向量相互正交
存在酉矩阵 U U H A U
Hermite二次型
定义
f ( X ) = X H A X = ∑ i = 1 n ∑ j = 1 n a ij x i x j
性质
若 A , B ∀ X ∈ C n , X H A X = X H BX A = B
设f ( X ) = X H A X , g ( Y ) = Y H B Y X = C Y f ( X ) = g ( Y ) B = C H A C
共轭合同
定义
设 A , B C B = C H A C A B
性质
反身性:A A
对称性:若 A B B A
传递性:若 A B B C A C
正规阵
定义
设 A ∈ C n × n A H A = A A H A
重要定理
若 A A
Hermite矩阵酉矩阵都是正规阵
A ∈ C n × n ⇔ A A ∈ C n × n ⇔ A n
Shur引理 :对于任意矩阵 A U U H A U
Hermite二次型的标准形
定义
假设 Hermite 二次型 f ( X ) X = C Y g ( Y ) = f ( X ) = Y H D Y g ( Y ) = d 1 ∣ y 1 ∣ 2 + d 2 ∣ y 2 ∣ 2 + ⋯ + d n ∣ y n ∣ 2 d i d 1 ≥ d 2 ≥ ⋯ ≥ d n
惯性定理
定义
若f ( X ) X = C Y X = D Z p q
定理
若 n × n A , B A , B
若 A 1 = a 1 ⋱ a p A 2 = b 1 ⋱ b q a 1 , ... , a p , b 1 , ... , b q
规范形
定义
如 n × n A p , q A I p 0 0 0 − I q 0 0 0 0 A
性质
r ( A ) = p + q
正定性和半正定性
定义
若对任意非零向量 X ∈ C n X H A X > 0 A
若对任意非零向量 X ∈ C n X H A X ≥ 0 A
正定矩阵的充分必要条件
A A A n 存在可逆矩阵 P A = P H P
A I
半正定矩阵的充分必要条件
A A A 存在矩阵 P A = P H P
重要定理
若 A A
若 A A − 1
若 A , B A + B
λ 多项式
定义:n F a 0 , a 1 , ... , a n ∈ F
f ( λ ) = a n λ n + a n − 1 λ n − 1 + ⋅⋅⋅ a 1 λ + a 0 称为数域上关于 λ
如果 a n = 0 a n λ n f ( λ ) n ∂ ( f ( λ )) ∂ ( f ( λ )) = n
如果 a 0 = a 1 = ・・・ = a n = 0 零多项式 ,规定 ∂ ( f ( λ )) = − ∞
如果 a 0 = 0 , a 1 = ・・・ = a n = 0 零次多项式 ,∂ ( f ( λ )) = 0
多项式的带余除法
定义:f ( λ ) , g ( λ ) ∈ F [ λ ] g ( λ ) = 0 q ( λ ) , r ( λ ) ∈ F [ λ ]
f ( λ ) = g ( λ ) q ( λ ) + r ( λ ) 其中,要么 r ( λ ) = 0 r ( λ ) = 0 ∂ ( r ( λ )) < ∂ ( g ( λ ))
q ( λ ) g ( λ ) f ( λ ) r ( λ )
如果 r ( λ ) = 0 g ( λ ) f ( λ ) g ( λ ) ∣ f ( λ )
多项式的公因式,公倍式
f ( λ ) , g ( λ ) , d ( λ ) ∈ F [ λ ] d ( λ ) ∣ f ( λ ) d ( λ ) ∣ g ( λ ) d ( λ ) f ( λ ) , g ( λ ) f ( λ ) , g ( λ ) , d ( λ ) ∈ F [ λ ] f ( λ ) ∣ d ( λ ) g ( λ ) ∣ d ( λ ) d ( λ ) f ( λ ) , g ( λ ) 最大公因式 GCD:次数最大的公因式
最小公倍式 LCM:次数最小的公倍式
如果 GC D ( f ( λ ) , g ( λ )) = 1 f ( λ ) g ( λ )
质因式分解
f ( λ ) = ( q 1 ( λ ) ) r 1 ( q 2 ( λ ) ) r 2 ⋅⋅⋅ ( q s ( λ ) ) r s 其中 q i ( λ ) q i ( λ ) q i ( λ )
类比实数域中的,任何一个合数都可以分解为几个质数的乘积
一个多项式是否可约,关键要看数域 F
F = R , λ 2 + 1 , 不可约 F = C , λ 2 + 1 = ( λ + i ) ( λ − i ) , 可约 常见数域的不可约多项式
R [ λ ]
aλ + b ( a , b ∈ R & a = 0 ) a λ 2 + bλ + c ( a , b , c ∈ R & a = 0 & b 2 − 4 a c < 0 ) C [ λ ]
aλ + b ( a , b ∈ C & a = 0 ) λ
以多项式为元素的矩阵称为多项式矩阵,简称为 λ F m × n [ λ ] m n λ F λ A ( λ ) ∈ F m × n [ λ ] A ( λ ) = [ a ij ( λ ) ] m × n a ij ( λ ) ∈ F [ λ ]
方阵 A λ I − A λ
A = ( a ij ) n × m λ I − A = λ − a 11 − a 21 ⋮ − a n 1 − a 12 λ − a 22 − a n 2 ⋯ ⋯ ⋯ − a 1 n − a 2 n λ − a nn 数字矩阵是 λ
以多项式为元素的矩阵和以矩阵为系数的多项式
如
A ( λ ) = [ λ 2 + λ + 1 2 λ λ − 1 1 ] 可以写成
A ( λ ) = [ 1 0 0 0 ] λ 2 + [ 1 2 1 0 ] λ + [ 1 0 − 1 1 ] 多项式矩阵和通常矩阵的主要区别在于:其元素所在的运算系统 —— 多项式环 F [ x ]
λ
λ r r ≥ r + 1
可逆的 λ
一个 n λ V ( λ ) ∈ F n × n [ λ ]
U ( λ ) V ( λ ) = V ( λ ) U ( λ ) = I n 这里 I n n U ( λ ) U − 1 ( λ )
**定理:**一个 n λ U ( λ ) det U ( λ )
注:n λ U ( λ ) n U ( λ ) U ( λ ) = [ λ 1 1 λ ]
Jordan 块
定义形如 J ( λ i ) λ i 1 λ i ⋱ ⋱ 1 λ i k × k Jordan 块 。Jordan 块是一个上三角矩阵,其主对角线上的元素均相等;主对角线上面一条斜线的元素均为 1;其余元素均为 0
特殊地,当 k = 1 [ λ i ]
Jordan 形矩阵
形如 J = J ( λ 1 ) J ( λ 2 ) ⋱ J ( λ s ) J ( λ i ) Jordan 形矩阵 。Jordan 形矩阵是一个分块对角阵,其中每一个小分块都是 Jordan 块
Jordan 标准形
若矩阵 A J J A
例 1
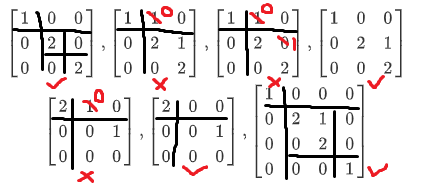
判断下列矩阵是否为 Jordan 形矩阵
1 0 0 0 2 0 0 0 2 , 1 0 0 1 2 0 0 1 2 , 1 0 0 1 2 0 0 0 2 , 1 0 0 0 2 0 0 1 2 2 0 0 1 0 0 0 1 0 , 2 0 0 0 0 0 0 1 0 , 1 0 0 0 0 2 0 0 0 1 2 0 0 0 0 1 **解:**对于正确的 Jordan 形矩阵,用黑线给出了分块形式;对于错误的 Jordan 形矩阵,指出了需要修改的元素
Jordan 标准形的存在性、唯一性
对矩阵 A
若 J = J 1 J 2 ⋱ J s A K = J i 1 J i 2 ⋱ J i s J i 1 , J i 2 , ... , J i s J 1 , J 2 , ... , J s K A
那么所谓的 Jordan 标准形的唯一性是如何定义的呢?除了相差 Jordan 块的次序外,矩阵的 Jordan 标准形是存在的、唯一的
性质
若 A J λ 0 k rank (( A − λ 0 E ) k ) = rank (( J − λ 0 E ) k )
若 n × n N = 0 1 0 ⋱ ⋱ 1 1 rank ( N k − 1 ) − rank ( N k ) = { 1 , 若 k ≤ n 0 , 若 k > n
若 J rank (( J − λ 0 E ) k − 1 ) − rank (( J − λ 0 E ) l ) J ≥ k λ 0
定理
设 λ 0 A A λ 0 k
rank ( B k − 1 ) − 2 ⋅ rank ( B k ) + rank ( B k + 1 ) 其中,B = A − λ 0 E
根据这个定理,我们只要针对矩阵 A λ 0 A 根据一个矩阵 A A − λ 0 E k A
Jordan 标准形的求法
求矩阵 A ∣ λ E − A ∣ = ( λ − λ 1 ) k 1 ( λ − λ 2 ) k 2 ... ( λ − λ s ) k s k i λ i 代数重数,决定了对角线上特征值 λ i ;
对 λ i ( A − λ i E ) X = 0 A 线性无关的特征向量 α 1 , α 2 , ... , α t i t i λ i 几何重数,决定了 Jordan 块的个数 ;
如果 k i = t i 代数重数等于几何重数 ,说明 λ i
如果 t i < k i α j ( A − λ i E ) = α j
将所有特征值 λ i J A
最小多项式 决定了关于 Jordan 块的最大尺寸。
Gram 矩阵
欧氏空间
V R
σ : V × V → R 对于 α , β ∈ V σ ( α , β ) ⟨ α , β ⟩ σ
对称性:⟨ α . β ⟩ = ⟨ β , α ⟩
(右)齐次性:⟨ α , k β ⟩ = k ⟨ α , β ⟩
(右)可加性:⟨ α , β + γ ⟩ = ⟨ α , β ⟩ + ⟨ α , γ ⟩
非负性:⟨ α , α ⟩ ≥ 0 ⟨ α , α ⟩ = 0 ⇔ α = 0
则称 �σ V 当 V (R n
实际上 α β ⟨ α , β ⟩ α β
实内积的性质
(左)齐次性:⟨ k α , β ⟩ = k ⟨ α , β ⟩
(左)可加性:⟨ α + β , γ ⟩ = ⟨ α , γ ⟩ + ⟨ β , γ ⟩
⟨ k 1 α 1 + ⋅⋅⋅ + k s α s , β ⟩ = k 1 ⟨ α 1 , β ⟩ + ⋅⋅⋅ k s ⟨ α s , β ⟩ ⟨ α , k 1 β 1 + ⋅⋅⋅ + k s β s ⟩ = k 1 ⟨ α , β 1 ⟩ + ⋅⋅⋅ k s ⟨ α , β s ⟩
复内积
V C
σ : V × V → C 对于 α , β ∈ V σ ( α , β ) ⟨ α , β ⟩ σ
共轭对称性:⟨ α . β ⟩ = ⟨ β , α ⟩
(右)齐次性:⟨ α , k β ⟩ = k ⟨ α , β ⟩
(右)可加性:⟨ α , β + γ ⟩ = ⟨ α , β ⟩ + ⟨ α , γ ⟩
非负性:⟨ α , α ⟩ ≥ 0 ⟨ α , α ⟩ = 0 ⇔ α = 0
则称 σ V 当 V (R n
复内积的性质
(左)齐次性:⟨ k α , β ⟩ = k ˉ ⟨ α , β ⟩
(左)可加性:⟨ α + β , γ ⟩ = ⟨ α , γ ⟩ + ⟨ β , γ ⟩
⟨ k 1 α 1 + ⋅⋅⋅ + k s α s , β ⟩ = k 1 ⟨ α 1 , β ⟩ + ⋅⋅⋅ k s ⟨ α s , β ⟩ ⟨ α , k 1 β 1 + ⋅⋅⋅ + k s β s ⟩ = k 1 ⟨ α , β 1 ⟩ + ⋅⋅⋅ k s ⟨ α , β s ⟩
线性组合的内积的矩阵表示
α 1 , ... , α s ; β 1 , ... , β t C V
⟨ k 1 α 1 + ⋅⋅⋅ + k s α s , l 1 β 1 + ⋅⋅⋅ + l t β t ⟩ = ( k 1 , ... , k s ) ⟨ α 1 , β 1 ⟩ ⋮ ⟨ α s , β 1 ⟩ ⋯ ⋱ ⋯ ⟨ α 1 , β t ⟩ ⋮ ⟨ α s , β t ⟩ l 1 ⋮ l t Gram 矩阵
α 1 , ... , α s ; β 1 , ... , β t C V
⟨ α 1 , β 1 ⟩ ⋮ ⟨ α s , β 1 ⟩ ⋯ ⋱ ⋯ ⟨ α 1 , β t ⟩ ⋮ ⟨ α s , β t ⟩ 称为 α 1 , ... , α s ; β 1 , ... , β t G ( α 1 , ... , α s ; β 1 , ... , β t )
α 1 , ... , α s C V
⟨ α 1 , β 1 ⟩ ⋮ ⟨ α s , β 1 ⟩ ⋯ ⋱ ⋯ ⟨ α 1 , β t ⟩ ⋮ ⟨ α s , β t ⟩ 称为 α 1 , ... , α s G ( α 1 , ... , α s )
α 1 , ... , α s C n A = ( α 1 , ... , α s )
G ( α 1 , ... , α s ) = A H A 其中,A H = ( A ˉ ) T = ( A T )
α 1 , ... , α s R n A = ( α 1 , ... , α s )
G ( α 1 , ... , α s ) = A T A α 1 , ... , α s ; β 1 , ... , β t C V α 1 , ... , α s β 1 , ... , β t
( α 1 , ... , α s ) = ( β 1 , ... , β t ) A 则
G ( α 1 , ... , α s ) = A H G ( β 1 , ... , β t ) A Gram 矩阵的性质
rank ( G ) = rank ( α 1 , ... , α s ) Hermite 性:G H = G
非负性:∀ x ∈ C s x H G x ≥ 0 G ⇔ α 1 , ... , α s
矩阵分解
矩阵的满秩分解
设 A ∈ C r m × n B ∈ C r m × r , C ∈ C r r × n
A = BC
C r r
实际上上述定理用文字描述就是,一个亏秩的矩阵可以分解成一个列满秩与行满秩矩阵的乘积
**证明:**因为 rank ( A ) = r A
A ≃ [ E r 0 ( m − r ) × r 0 r × ( n − r ) 0 ( m − r ) × ( n − r ) ] = [ E r 0 ( m − r ) × r ] [ E r 0 r × ( n − r ) ] 因此存在两个可逆矩阵 P , Q P A Q = [ E r 0 0 0 ]
A = P − 1 [ E r 0 ] [ E r 0 ] Q − 1 ≜ BC 因为 P − 1 [ E r 0 ] B = P − 1 [ E r 0 ] C = [ E r 0 ] Q − 1
矩阵满秩分解的计算
如何在给定矩阵 A B , C
设
A = [ α 1 , α 2 , ... , α n ] B = [ β 1 , β 2 , ... , β r ] , 其中 β 1 , ... , β r 线性无关 所以
A = BC ⇒ [ α 1 , α 2 , ... , α n ] = [ β 1 , ... , β r ] c 11 ⋮ c r 1 ⋯ ⋱ ⋯ c 1 n ⋮ c r n 实际上我们可以取 β 1 , ... , β r α 1 , ... , α n B A C A
例 1
求矩阵 A = 1 2 − 1 2 4 0 2 6 − 1 0 − 4 − 5 5 0 0 5 6 − 14 1 − 7
**解:**对矩阵 A
A = 1 2 − 1 2 4 0 2 6 − 1 0 − 4 − 5 5 0 0 5 6 − 14 1 − 7 → ⋅⋅⋅ → 1 0 0 0 0 1 0 0 0 0 1 0 0 7 10 7 5 0 − 7 7 29 7 25 0 A
B = 1 2 − 1 2 4 0 2 6 − 1 0 − 4 − 5 , C = 1 0 0 0 1 0 0 0 1 0 7 10 7 5 − 7 7 29 7 25 例 2
求矩阵 A = 2 2 1 1 5 3 − 2 − 1 − 1 3 4 2 1 1 1
**解:**对矩阵 A
A = 2 2 1 1 5 3 − 2 − 1 − 1 3 4 2 1 1 1 → ⋅⋅⋅ → 1 0 0 0 1 0 0 0 1 5 8 5 1 5 1 − 5 2 5 1 − 5 4 A
B = 2 2 1 1 5 3 − 2 − 1 − 1 , C = 1 0 0 0 1 0 0 0 1 5 8 5 1 5 1 − 5 2 5 1 − 5 4 QR 分解的应用
请用 QR A x = b A x = A − 1 b A − 1 A QR x = b
{ Q y = b R x = y 因为 Q Q − 1 = Q H y = Q H b
由于 R R = r 11 ⋯ r 22 ⋯ ⋱ r nn
r 11 ⋯ r 22 ⋯ ⋱ r nn x 1 ⋮ x n = y 1 ⋮ y n ⇒ ⎩ ⎨ ⎧ x n = r nn y n x n − 1 = r n − 1 , n − 1 y n − 1 − r nn x n ⋮ 例 3
用 QR A x = b A = − 3 1 1 1 1 1 − 1 − 1 2 1 0 1 , b = 1 0 − 2 1
**解:**将 A = ( α 1 , α 2 , α 3 ) α 1 , α 2 , α 3
v 1 v 2 v 3 = ( − 12 3 , 12 1 , 12 1 , 12 1 ) T = ( 0 , 6 2 , − 6 1 , − 6 1 ) T = ( 0 , 0 , − 2 1 , 2 1 ) T 令 Q = ( v 1 , v 2 , v 3 )
R = Q H A = 2 3 0 0 − 3 2 6 4 0 3 4 6 1 2 1 R − 1 = 6 3 0 0 12 6 4 6 0 − 4 3 2 − 4 2 2 所以
x = R − 1 Q H b = − 4 1 0 0 4 1 2 1 0 4 3 0 − 1 − 4 3 − 2 1 1 1 0 − 2 1 = − 2 5 − 2 1 3 矩阵的 LU 分解
LU 分解(LU Decomposition)是矩阵分解的一种,可以将一个矩阵分解为一个单位下三角矩阵和一个上三角矩阵的乘积,以四阶矩阵为例
L = 1 ∗ ∗ ∗ 0 1 ∗ ∗ 0 0 1 ∗ 0 0 0 1 , U = ∗ 0 0 0 ∗ ∗ 0 0 ∗ ∗ ∗ 0 ∗ ∗ ∗ ∗ LU 矩阵是否一定存在?答案是否,具体看下面的例子
设 [ 0 1 1 0 ] = [ a b 0 c ] [ l 0 m n ]
⎩ ⎨ ⎧ a l = 0 am = 1 b l = 1 bm + c n = 0 由 a l = 0 a = 0 l = 0
**LU 分解定理:**设 A ∈ C n n × n A ⇔ A Δ k = 0 , k = 1 , 2... , n
k k × k
将矩阵 A L U A x = b A = LU ( LU ) x = b ⇒ L ( Ux ) = b ⇒ { L y = b Ux = y
所以 x = U − 1 y = U − 1 L − 1 b
LU 矩阵的求法
实际上 LU 矩阵有非常多的求法,这里我举一种比较简单的待定系数法
设 A = 2 1 1 3 1 2 4 9 − 6 A L U
**解:**令
L = 1 l 1 l 2 0 1 l 3 0 0 1 , U = u 1 0 0 u 2 u 4 0 u 3 u 5 u 6 由于 A = LU
⎩ ⎨ ⎧ u 1 = 2 u 2 = 3 u 3 = 4 l 1 u 1 = 1 l 1 u 2 + u 4 = 1 l 1 u 3 + u 5 = 9 l 2 u 1 = 1 l 2 u 2 + l 3 u 4 = 2 l 2 u 3 + l 3 u 5 + u 6 = − 6 上面的方程组非常容易解,最后求出
L = 1 2 1 2 1 0 1 − 1 0 0 1 , U = 2 0 0 3 − 2 1 0 4 7 − 1 矩阵的 SVD 分解
**SVD 分解定理:**设 A ∈ C r m × n
对 rank ( A ) = r A A H A 非零特征值 有 λ 1 ⩾ λ 2 ⩾ ・・・ ⩾ λ r > 0 正数 σ i = λ i A
存在酉矩阵 U , V U − 1 A V = Σ = σ 1 0 ⋱ σ n 0 0 m × n σ 1 ≥ σ 2 ≥ ・・・ ≥ σ r > 0
SVD 分解的求法
由特征多项式 ∣ λ E − A H A ∣ = 0 λ 1 ⩾ λ 2 ⩾ .. ⩾ λ n 务必�按照从大到小排列 ),以及每个特征值对应的特征向量 ( α 1 , α 2 , ... , α n )
对特征向量进行施密特正交化和单位化,得到单位正交向量组 V = ( v 1 , v 2 , .. , v n )
对于非零特征值 λ 1 , ... , λ r σ 1 , ... , σ r u i = σ i 1 A v i r u r + 1 , ... , u n u i T x = 0 u i
于是得到 A = U Σ V H
实际上 A H A 半正定矩阵 ,其特征值一定非负
例 4
已知 A = 1 0 0 2 0 0 A
**解:**因为 A H A = 5 0 0 0 0 0 0 0 0 A H A 5 , 0 , 0 A 5
例 5
已知 A = 1 0 1 1 0 1 A U V
解: A H A = [ 2 2 2 2 ] A H A λ 1 = 4 , λ 2 = 0 α 1 = [ 1 , 1 ] T , α 2 = [ − 1 , 1 ] T
v 1 v 2 = [ 2 1 , 2 1 ] T = [ − 2 1 , 2 1 ] T 于是有
V = [ 2 1 2 1 − 2 1 2 1 ] 因为 u 1 = 2 1 A v 1 = 2 1 0 2 1 u 1 T x = 0
x 1 x 2 = u 2 = 2 1 0 − 2 1 = u 3 = 0 1 0 故
U = 2 1 0 2 1 2 1 0 − 2 1 0 1 0 验算可得 U − 1 A V = Σ
例 6
求 A = [ 1 1 1 1 1 1 ]
解: A H A = 2 2 2 2 2 2 2 2 2 A H A λ 1 = 6 , λ 2 = λ 3 = 0 α 1 = [ 1 , 1 , 1 ] T , α 2 = [ 1 , 0 , − 1 ] T , α 3 = [ 0 , 1 , − 1 ] T
v 1 v 2 v 3 = [ 3 1 , 3 1 , 3 1 ] T = [ 2 1 , 0 , − 2 1 ] T = [ − 6 1 , 3 6 , − 6 1 ] T 于是有
V = 3 1 3 1 3 1 2 1 0 − 2 1 − 6 1 3 6 − 6 1 因为 u 1 = 6 1 A v 1 = [ 2 1 2 1 ] u 1 T x = 0
x 1 = u 2 = [ 2 1 − 2 1 ] 故
U = [ 2 1 2 1 2 1 − 2 1 ] 验算可��得 U − 1 A V = Σ