Cramer-Rao Lower Bound
参数估计
什么是参数估计问题?
设未知参数,估计器模型的估计量为 如,衡量一个估计器(estimator, 也称估计量或估计算法)的性能,主要考量以下三个方面:
- 无偏性(unbiased)。满足的估计量为无偏估计量。
- 有效性(availability)。刻画估计量到真实值的偏离程度,。 若存在多种无偏估计器,我们称 估计量方差最小 的估计器是最有效的。
- 一致性(consistency)。当样本数时,对于任意的,有= 1\hat{\theta}\theta$ 是一致的。 一致性所体现的是,当样本总数逐渐增加时,估计量逐渐收敛于真实值。
上述三点考量,我们来看第二点:如何衡量一个无偏估计器是否是有效的?
——统计信号处理理论中的 克拉美-罗下界(Cramer-Rao Lower Bound,CRLB) 就是衡量一个无偏估计器的有力工具。
举一种最简单的情况:
一个物理量为,我们使用某种方式去观测它,观测值为,由于存在噪声,此时 , 为高斯噪声。由于我们很自然地会直接使用观测值去估计,所以这时候就会存在估计误差。直观地理解,噪声的方差越大,估计就可能越不准确。
为什么要讨论克拉美-罗界?
上面例子的方式,使用 去估计 ,
按第1个标准,它是无偏的,估计值会在真实值附近波动;
按第2个标准,这个估计值波动的剧烈程度,也就是方差。在这个例子里,克拉美-罗界就等于方差。
为什么不直接讨论方差而要去计算克拉美-罗界呢?
因为方差是针对某一种特定的估计量(或理解为估计方式)而言的,上面的例子中方差是估计量 的方差,在更复杂的问题里,对 可以有各种不同的估计量,他们分别的方差是不同的,显然,对于无偏估计量而言,方差越小的估计方式性能越好,但是这些方差都有一个下界,就是克拉美-罗界。
直观地理解克拉美-罗界
克拉美-罗界本身不关心具体的估计方式,只是去反映:利用已有信息所能估计参数的最好效果。
还是上面那个参数估计的例子:
我们用 估计真实值 ,,高斯噪声 ,所以也可以认为 ,也就是说:
当我们观察到的时候,可以知道真实值的概率密度分布(pdf)是以 为均值,为方差的正态分布,即 ,
下面两幅图给出两个似然函数的例子:
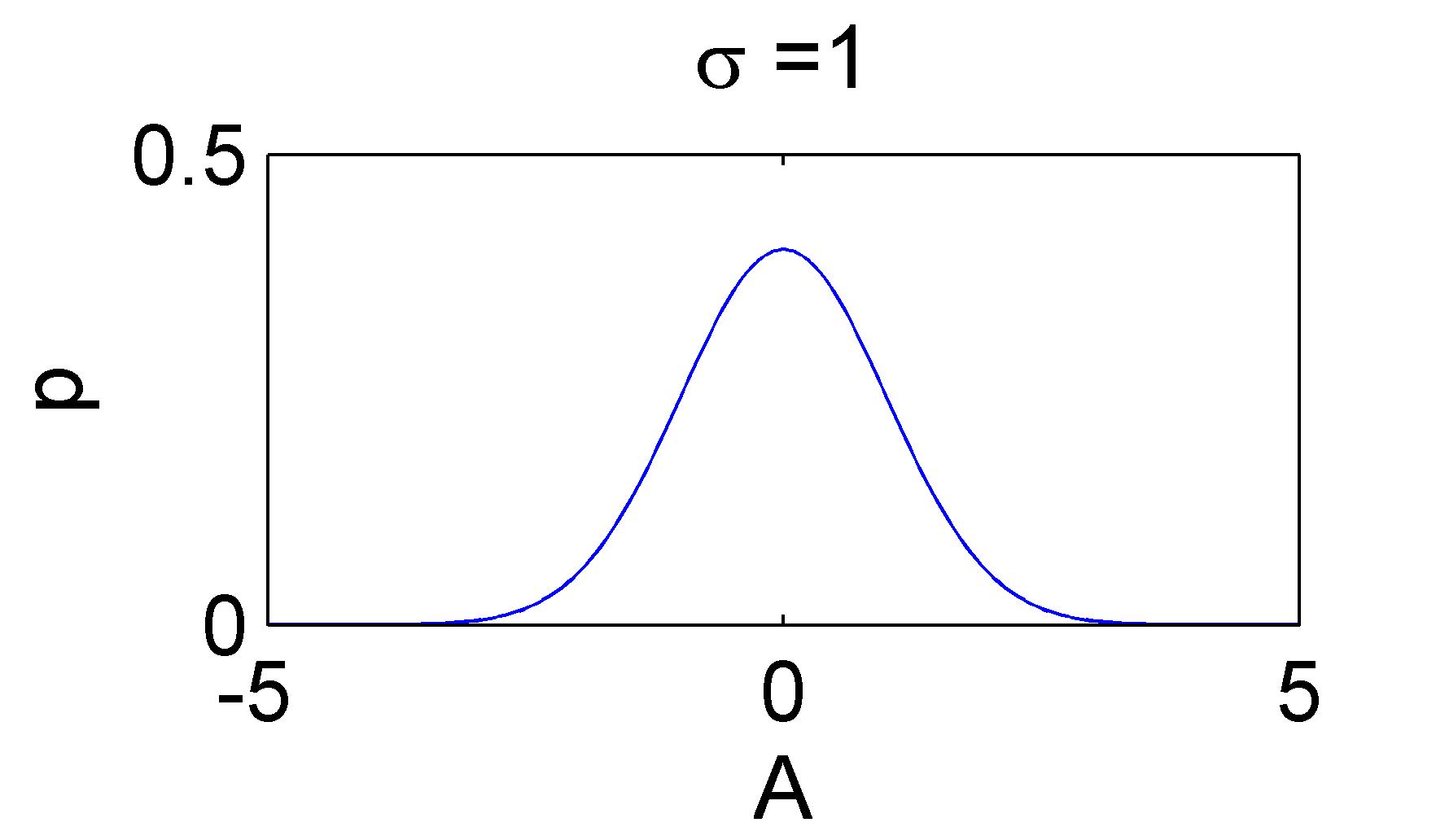
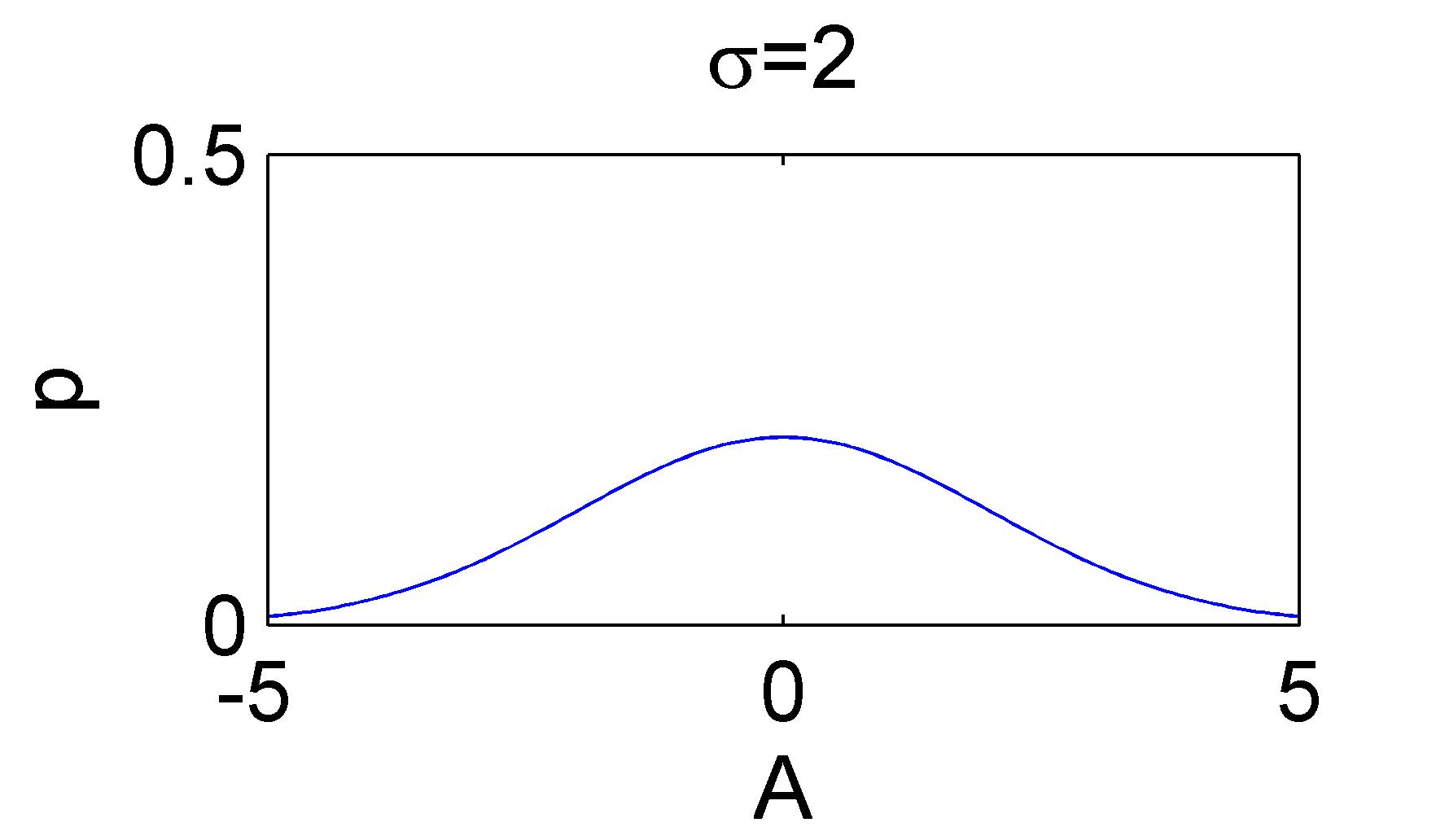
似然函数;在观测到样本的情况下,参数是的可能性。
在这里,似然函数表示:在我观测到 的情况下,我要估计的参数 的可能性是多少?
似然函数的值 = 已知真实的参数 的情况下,观测到 的概率(即概率密度函数)
直观地看,似然函数的“尖锐”性决定了估计参数的精度。
这个“尖锐”性可以用 对数似然函数峰值处的 负的 二阶导数 来度量,即对数似然函数的曲率。(用对数是为了便于计算。)曲率越大,越“尖锐”。
这里算出来的结果为 ,是噪声的方差的倒数。也就是说噪声越小,曲率越大,对数似然函数越尖锐。
似然函数:
取对数:
对参数 求一阶导:
对参数 求二阶导:
再取负号得:
不同的估计量(估计方式)的含义
举一个稍微复杂一点点的参数估计问题:
一个物理量为 ,我们使用某种方式去观测它,第一次观测值为 ,第二次观测值为 ,这是两个不同时刻的观测结果,一样的高斯噪声 。
这时候不同的人不同的考虑方式可能产生不同的估计方式,例如:
- 甲:采用估计量 ,即两次观测的平均;
- 乙:可能觉得甲的计算量有点大了,直接采取估计量 ;
- 丙:可能认为第二次观测值可能会受到系统影响而不准确,他更相信前面的观测值,于是采取估计量
上述三个估计量都是无偏的,来看下他们各自的方差:
- 甲估计量的方差:
- 乙估计量的方差:
- 丙估计量的方差:
可以发现,甲估计量的方差最小,他的估计效果较好。
但是!如果第二个观测值真的不太准确,也就是后一个高斯噪声比较大,那有可能就是丙估计量更加合适了!
所以,对同一个待估计值,不同估计方式产生的方差是不一样的.
但是数学家们已经证明了:任何无偏估计量的方差必定大于等于克拉美-罗界。
克拉美-罗界的基本计算
假设两次观察相互独立,仅受相同的高斯白噪声影响,则真实参数A AA的似然函数应该为两个正态的概率密度分布相乘:
计算出来的对数似然函数的曲率为
两次观测:
似然函数:
取对数:
一阶导:
二阶导:
取负号:
实际上,当观测样本数为时,这个值为 —— 观测样本数越多,获取的信息越多,曲率越大,对数似然函数越"尖锐"。
这个二阶导数(曲率)更一般的度量是(下面用 来表示要估计的参数):
——它度量了对数似然函数的平均曲率(很多情况下曲率与有关,所以取数学期望使它仅为的函数),,
——被称为数据 的 Fisher信息 ,,——具有信息测度的基本性质(非负性、独立观测的可加性)
一般来说,Fisher 信息的倒数就是⭐克拉美-罗界了!任何无偏估计量 的方差满足:
我的理解是:
- Fisher信息值是所有无偏估计方案中方差最小的一个(最有效的一个),是所有无偏估计量的方差的下界,,
- 任何一个无偏估计量的方差都不会比它小,,也就是不会比它更好,离它越近表示估计越好,越有效
- 另外,🍎信息越多,Fisher信息值越大,这个下界越低,表示估计越有效!
克拉美-罗界 正式定义
克拉美-罗界的标准定义 【定理】Cramer-Rao 下界——Scale Parameter(标量参数)
对于估计的参数 为标量时, 假定PDF 满足“正则”条件(对所有的 ):
其中数学期望是对 求取的。
那么,任何无偏估计量 的方差必定满足:
其中导数是在 的真值处计算的,数学期望是对 p ( x ; θ ) p(x;\theta)p(x;θ) 求取的。
而且,对于某个函数 和 ,当且仅当 时,对所有 达到下限的无偏估计量就可以求得。这个估计量是 ,它是MVU估计量(最小方差无偏估计),最小方差是 。
小结 估计一个参数,根据已有信息得到了似然函数(或者pdf),这个pdf的“尖锐”性,或者,符合似然函数分布的这组数据的方差,就是克拉美罗界,它可以通过对对数似然函数求二阶导再取负号再取倒数得到。
克拉美罗界的计算不依赖具体的估计方式,它可以用来作为一个衡量估计方式好坏的标准——估计量的方差越靠近克拉美罗界,效果越好。
在参数估计和统计中,Cramer-Rao界限(Cramer-Rao bound, CRB)或者Cramer-Rao下界(CRLB),表示一个确定性参数的估计的方差下界。
它的最简单形式是:任何无偏估计的方差至少大于Fisher信息的倒数。
一个达到了下界的无偏估计被称为 完全高效的(fully efficient)。这样的估计达到了所有无偏估计中的最小均方误差(MSE,mean square error),因此是最小方差无偏(MVU,minimum variance unbiased)估计。