基本概念
数学知识
随机变量(Random Variable)

统计学中往往用字母的大小写来区分随机变量和观测值,例如 X 表示随机变量,x 表示观测值
概率密度函数(Probability Density Function)

概率密度函数(Probability Density Function)有这样的性质:

期望(Expectation)
简单来说,对某一随机变量求期望就是在求它的平均。有微积分基础的可以理解:对于连续的随机变量可以采用求某一段积分来获得期望;而对于离散的随机变�量只需求和公式即可。
期望(Expectation)有如下性质:

随机抽样(Random Sampling)
举个例子,对于某一随机变量 X,可能 X 产生的值有 ['R', 'G', 'B'],那么随机抽样的过程就是在 X 可能产生的值 ['R', 'G', 'B'] 抽取的过程
专业术语(Terminology)
状态和动作(State and Action)
状态(State s)
Agent(智能体)在某一时刻 t 所处的状态,即为 State s,常常记为

动作(Action a)
Agent(智能体)在某一时刻 t 进入状态,做出相应的动作,即为 Action a ,常常即为
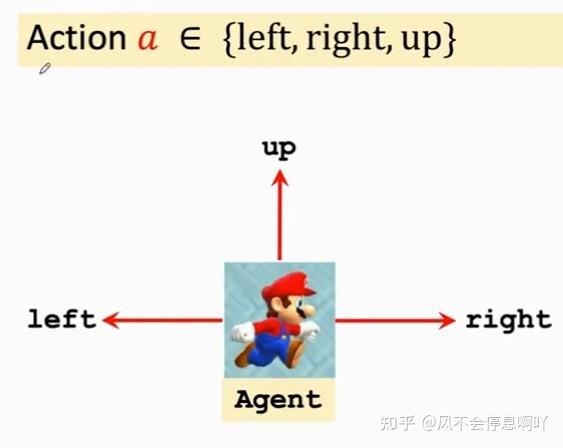
策略(Policy )
在数学上,策略是一个概率密度函数(Probability Density Function),在某一状态时,策略控制 Agent 做出动作,这里做出的动作是随机抽样得到的。

奖励(Reward)
Agent 在某一状态中做出一个动作,就会获得一个奖励

状态转移(State Transition)
一个状态转移到另一个状态的过程叫做状态转移
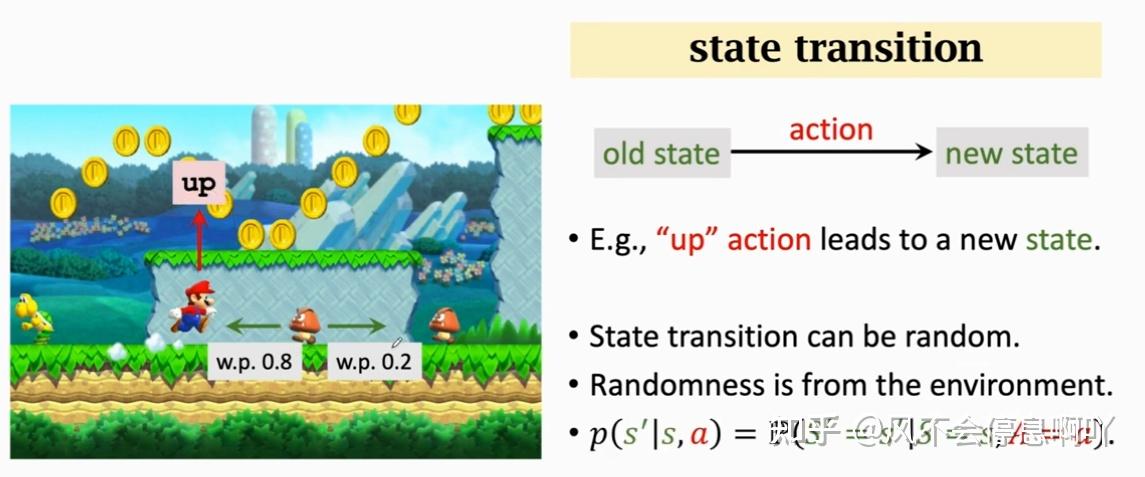
智能体环境交互过程
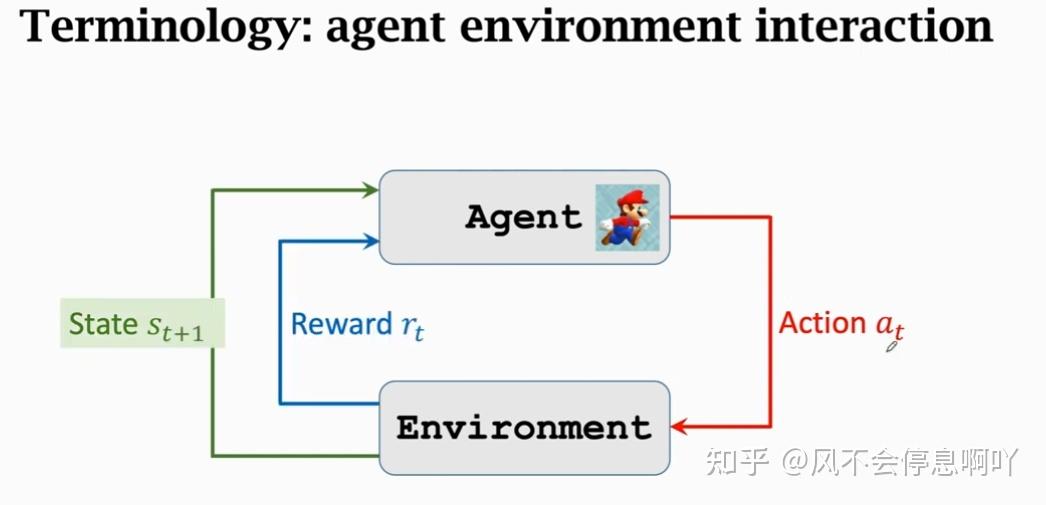
强化学习中的两种随机性
策略对动作进行随机抽样,状态转移函数对状态进行随机抽样

强化学习的训练过程(一个 trajectory)

回报(Return)
定义为:未来奖励的总和(Cumulative Future Reward),记作 ,由于每一步我们并不知道 的大小, 因此是随机变量

由于未来奖励的不确定性,因此强化学习中往往采用折扣回报
定义为:折扣性未来奖励的总和(Cumulative Discounted Future Reward)

回报的随机性(Randomness in Returns)
由于回报取决于奖励,而奖励又是由 Agent 所进入的状态和做出的动作进行打分而得到的,上文已经提到了在强化学习中状态和动作均具有随机性,因此回报(Return)也具有随机性。

动作价值函数(Action-Value Function)
上面讲到了, 是一个随机变量,依赖于未来所有的动作 A 和状态 S,因此为了无法评估当前形势。故引入动作价值函数,用对 求期望,用积分将随机性积掉,这样就能得到一个实数,用于评估形势。
期望的求取方法:将 当成未来所有状态 A 和 S 的一个函数,所以除了当前的动作 和状态 ,其余所有的状态和动作都被积掉了,因此这里的对于策略 的动作价值函数 只取决于当前的动作 和状态 的观测值

最优动作价值函数(Optimal Action-Value Function):能让动作价值函数 最大化的那个
, 这里与 无关

对于动作状态价值函数的理解

10)状态价值函数(State-Value Function)
可以告诉我们当前的形势的好坏

这里的 需要区分连续动作和离散动作:
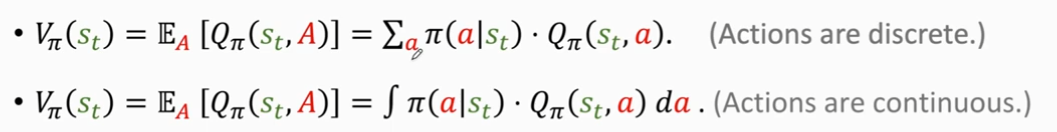
对于状态价值函数的理解:

如何利用 AI 的强化学习控制智能体训练
价值学习(Value-Based Learning)
采用最优动作价值函数

策略学习(Policy-Based Learning)
采用策略

总结(summary)
直接附上王树森大神的 Summary 的图:

强化学习的一个总体过程:
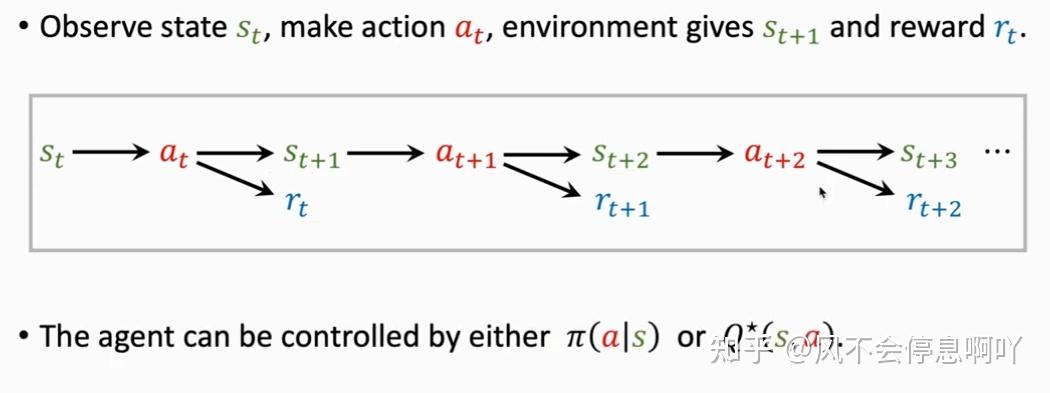
价值学习 Value-Based Learning
深度 Q 网络(Deep Q-Network DQN)
近似 Q 函数(Approximate the Q* Function)
可以被看成一个先知,它可以告诉 Agent 如何选择一个最好的动作 a,但 并不知道,因此这里需要近似
DQN 是一种价值学习的方法,利用一个神经网络(Neural Network NN)去近似一个 ,记为

对于不同问题,DQN 也许不一样,以超级玛丽为例:
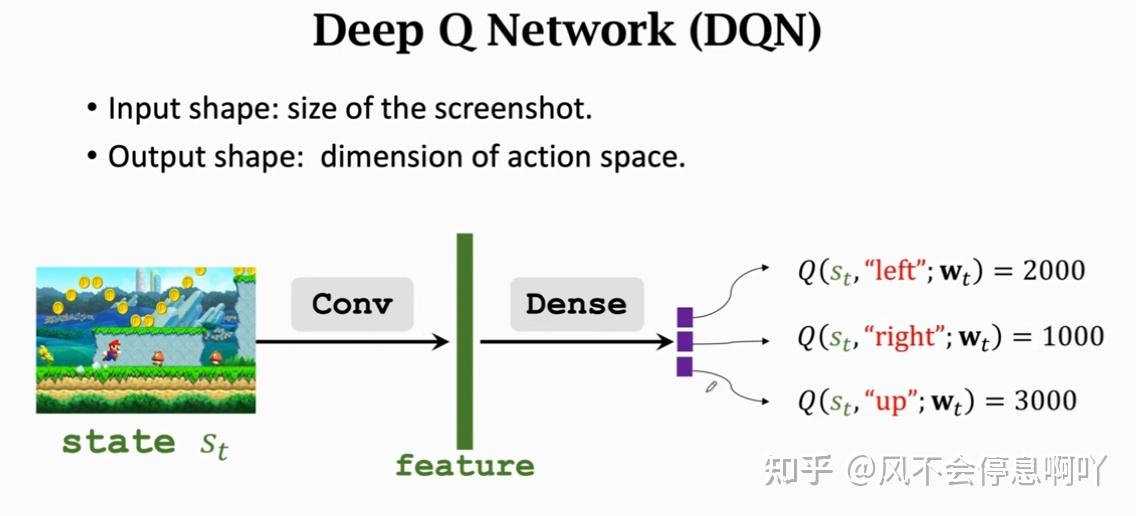
DQN 的训练 Agent 的一个 trajectory 如下图:
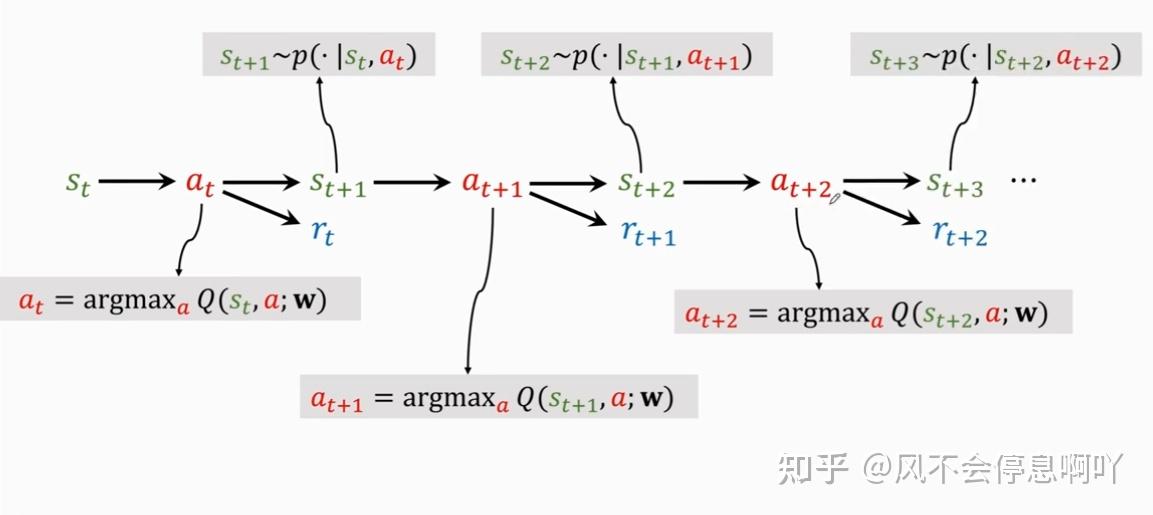
2)时序差分方法(Temporal Difference Learning TD-Learning)
例子:如果我想要从纽约到亚特兰大,且模型 预测了消耗的时间是 1000 分钟,这个模型一开始是随机的。
那么如何更新模型,使模型的预测值变得越来越准确?
① 首先做出一个预测:q = Q(w) → q = 1000
② 完成这段路程得到真实��值 y:y = 860
这时,产生了一个偏差(q-y)
我们记损失 Loss 为:,即 L2 范式,前面的 1/2 可以理解为方便计算梯度,线性变换并不会影响数据整体的相对值,例如,1 相对于 2 是 1/2 倍的关系,0.5 相对于 1 是 1/2 倍的关系。
那么,为了是预测值尽可能的逼近真实值,我们必须需要让 Loss 取到最小值。因此这里就引入了 L 对 w 的梯度 Gradient,也可以认为是求导。使用偏微分的链式法则,我们可以推导出 L 对 w 梯度的表达式,如下图所示:

这样,我们在进行参数更新时,采用梯度下降算法(Gradient Descent)即可使参数 w 不断接近真实值对应的参数 。
而现在,若到达不了目的地,不获取到真实的全路程的真实值,就可以利用 TD 算法来更新模型参数。
假设我们从纽约想亚特兰大出发,途中经过华盛顿,而在华盛顿停住不走,那么此时的预测就不再能使用整条路的真实值来更新预测值了。
因此,这里采用 TD 算法
我们已知模型做出一个预测:q = Q(w) → q = 1000
而从我们从纽约经过华盛顿停住不走,那么便有一个从纽约到华盛顿的真实值:y1 = 300
而从华盛顿到亚特兰大有一个模型预测值:q1 = Q(w1)→q = 600
那么此时我们定义 TD target 为 y = y1+q1 = 900, 这里的 TD target 比原本的模型预测值 1000 更加可靠。
我们记损失 Loss 为:L = 1/2*(q-y)²,定义 TD error 为 δ = q-y = 1000-900;此处也可以理解成模型对纽约到华盛顿的预测值为 400,而真实值是 300,δ = 400-300 = 100
类似地,我们可以得到 Loss Function 关于 w 的一个函数,对 w 求梯度,得到 Loss 的最小值对应的 w 用于更新参数(采用梯度下降方法 Gradient Descent)

我们必须使 TD error 尽可能地小,当 TD error = 0 时,那么我们就获得了最优的模型
TD Learning+DQN
如何将 TD 算法用于学习 DQN
对于上述例子,我们有了这样的方程
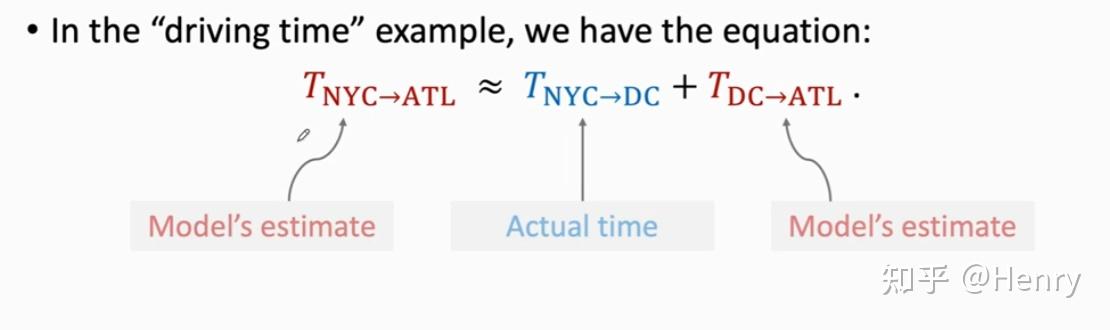
类似地,在深度强化学习中,有如下方程,即是用 TD 算法学习 DQN 的方程:

其中,方程左边是 DQN 在 t 时刻对状态和动作 进行的一次估计;等式右边是在 t 时刻真实观测到的奖励,以及 DQN 在 t+1 时刻对于状态和动作 进行的一次估计。
推导如下:

因此,将 TD 算法与 DQN 结合:

等式左边可以认为是模型对于时刻 t 关于参数 w 的预测值(Prediction);右边则是真实值+模型对于时刻 t+1 关于参数 w 的预测值,和式记为 TD target。
个人理解,这是一个贝尔曼方程,具体可以参照 忆臻:马尔科夫决策过程之 Bellman Equation(贝尔曼方程)
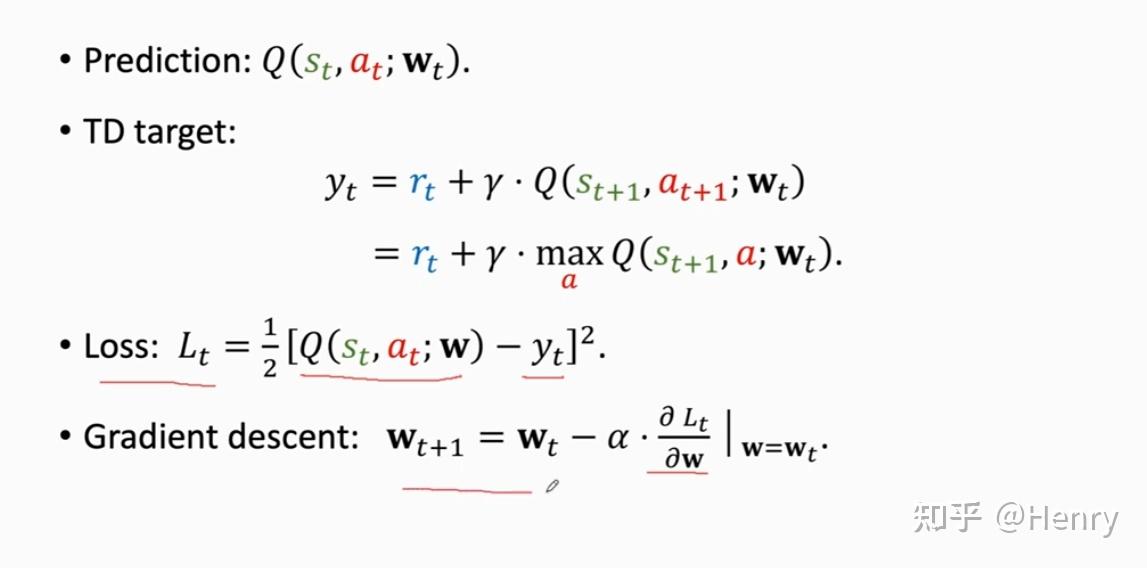
总结(Summary)

TD 算法用于学习 DQN 的一次迭代:

多次进行迭代,最后就可以将 TD error 逐渐减小;换句话说,模型预测值越来越接近 TD target。
策略学习 Policy-Based Learning
策略函数近似(Policy Function Approximation)
策略函数(Policy Function)
策略函数(Policy Function) 是一个概率密度函数,其输入是某个状态 s,输出是在该状态下可能产生的动作 a 的概率值。假设在状态 st 下,Agent 可能做出的动作 at 可能有 n 个,那么 即输出一个 n 维向量,其元素对应每个可能做出动作 at 的概率值。有了这 n 个概率值,Agent 就会在这个向量中做一次随机抽样(Random Sampling),并做出随机抽样所得的动作

策略网络(Policy Network)
策略网络(Policy Network) 则是使用了神经网络去近似策略函数 ,其中 是神经网络中的一个可训练参数
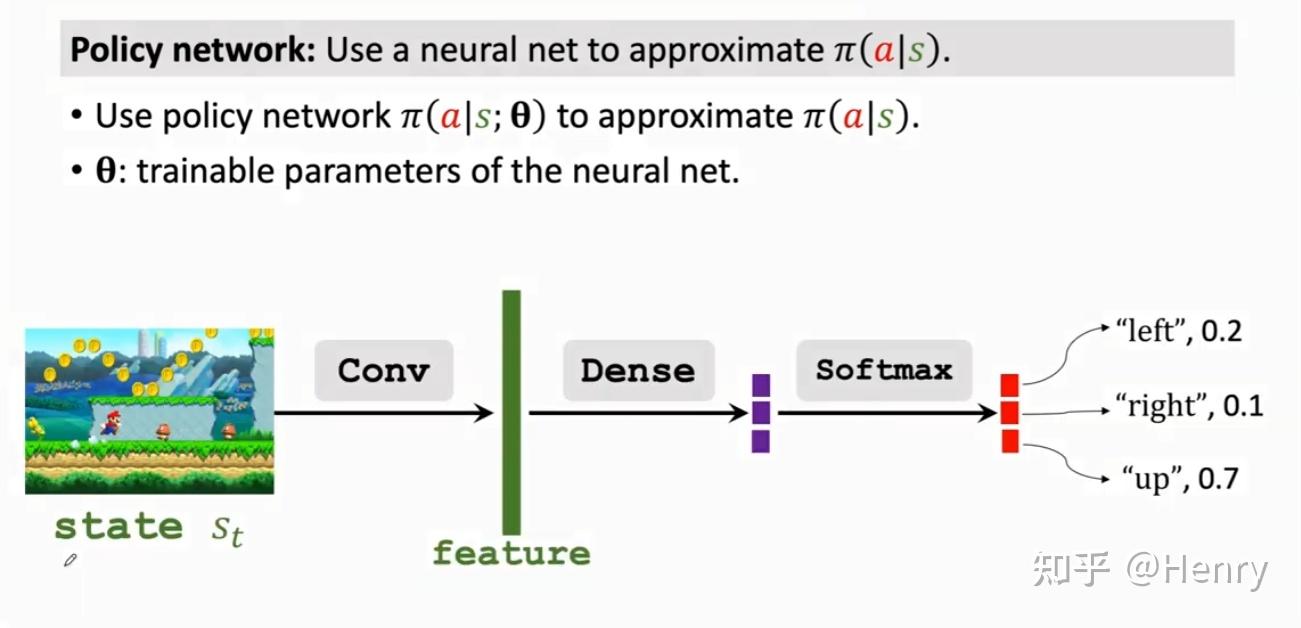
策略网络(Policy Network) 有着如下性质:

由于策略网络对于在动作空间 A 中所有可能取到的 a 所对应的概率之和必须等于 1,因此在策略网络的最后一层必须加上一个 Sotmax 这个 Activation Function。
状态价值函数近似(State-Value Function Approximation)
状态价值函数(Action-Value Function)
首先回顾上一章的三类函数:

这里注意:式 3 表示离散动作的期望求法;若为连续动作,则对动作空间中的所有 a 进行积分。
类比 State-Value Function 和 Approximation State-Value Function,区别在于:将策略 换成了策略网络

V 可以评价状态 s 和策略网络 的好坏。若给定状态 s,策略网络越好,那么 V 的值越大。因此,我们采用 V 关于 的随机梯度上升的方法更新参数 ,则有以下定义:

这类方法即策略梯度上升的方法,这里我们定义策略梯度(Policy Gradient)是近似状态价值函数 关于 的梯度。
策略梯度(Policy Gradient)
这里放上策略梯度的推导:
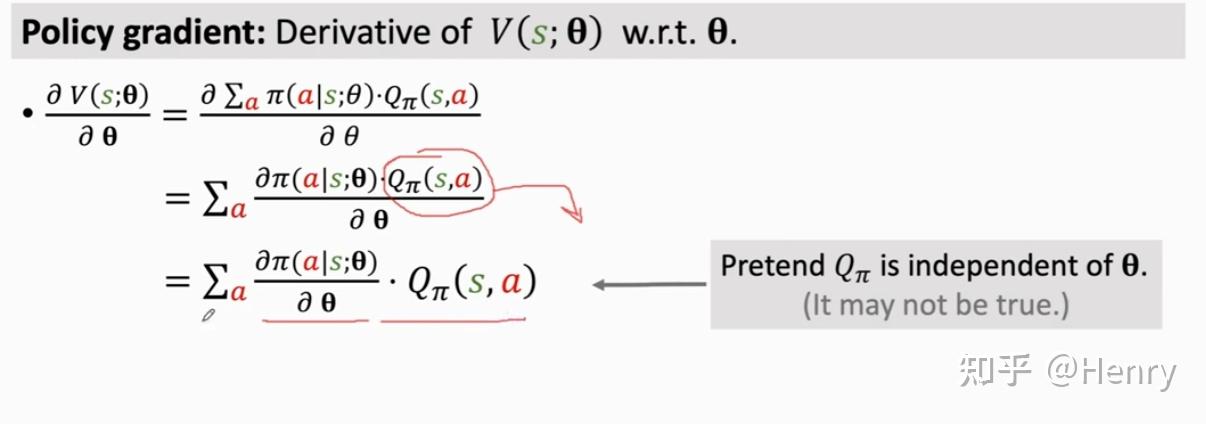
这里假��设 不依赖于 ,因此能够相当于一个常数提出来。但在实际中,由于 依赖于 ,而 是由神经网络参数 所决定的,因此往往 不能被提出。
因此,策略梯度的一种形式可以被写成如下形式:
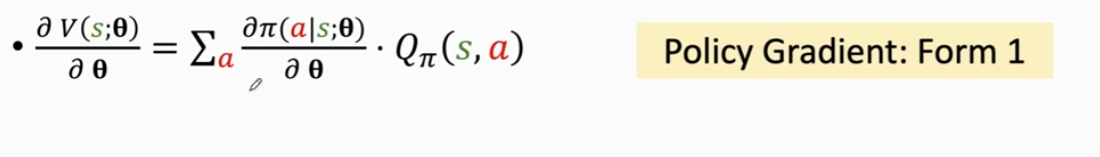
这里,如果动作 a 是离散的,那么只需要对 a 进行连加就可以将策略梯度算出来。
然而实际应用中往往不会用这个公式来计算策略梯度,而是使用蒙特卡洛近似的方法来近似。
这里对蒙特卡洛近似推导:

这里,有必要解释一下,这里利用了 log 函数的求导性质,有微积分基础的应该没什么问题,如果仅有高中水平的朋友可以自己上手求一下导,正着看或许有点问题,可以反过来推导,如上图紫色字体。

至此,我们证明了这两项是相等的:

这里我们就可以使用蒙特卡洛近似,推导出如下等式:

上面提到了这个推导不严谨,原因是因为 与策略 有关,因而与神经网络参数 有关,但事实上,最后的 对 也求偏导,最后也能得到这个式子。
至此,我们得到了策略梯度的两种等价形式:

对于离散的动作,我们可以采用第一种形式:

由于第一种形式的使用对象的局限性,因而第二种形式比第一种形式更为常用,这里举了连续动作的一种策略梯度的例子:

显然,这里对 关于 A 求期望就是策略梯度;且 是根据策略 中随机抽样得到的,故 是策略梯度的一个无偏估计。因此,我们就可以利用 去近似策略梯度,即蒙特卡洛近似(Monte Carlo Approximation)。具体推导可以参考 蒙特卡洛近似。
使用策略梯度更新策略网络

那么我们如何估计动作价值函数 ?
给出了这两种方法:
REINFORCE:必须获取到一个完整的 trajectory 才能进行一次模型参数的更新,也就是蒙特卡罗方法(MC Method)来估计 Q

Actor-Critic(AC):使用另一个神经网络来近似

总结(Summary)

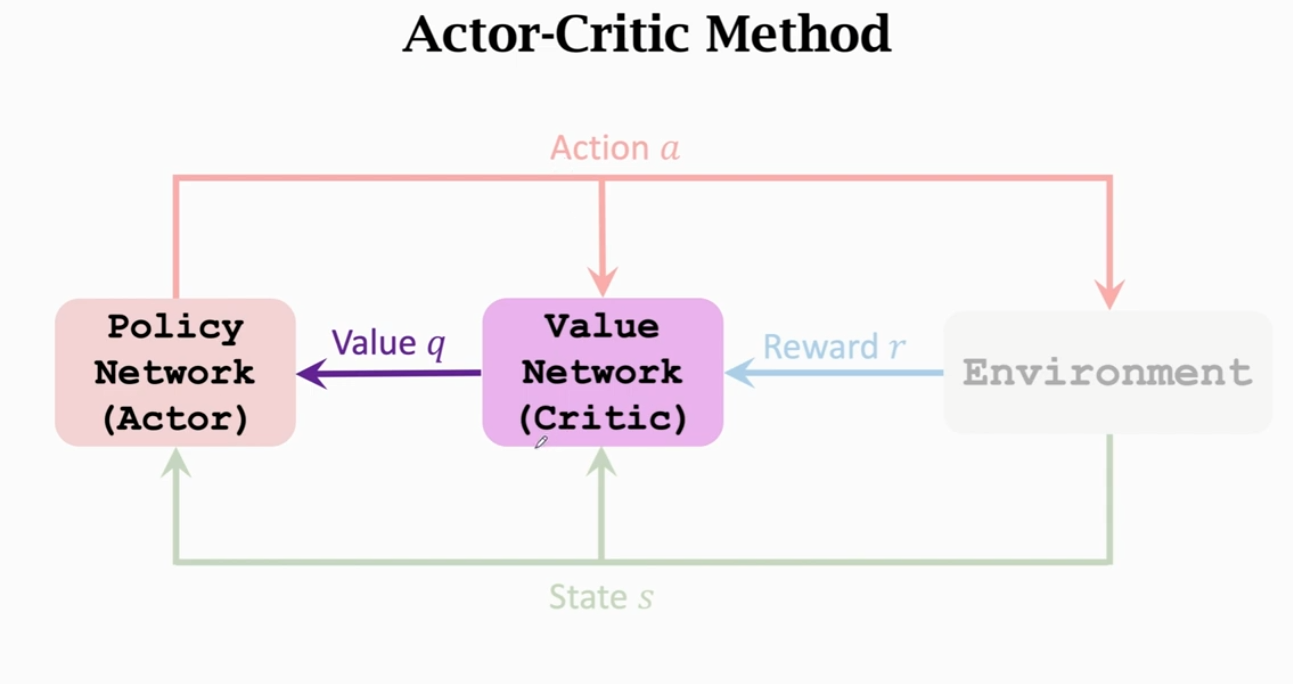
Actor-Critic Method(AC Method)
Actor-Critic 方法,是策略学习和价值学习结合的一种方法。
Actor 是策略网络,用来控制 Agent 运动�,可以看做“运动员”。
Critic 是价值网络,用来给动作打分,可以看做“裁判”。
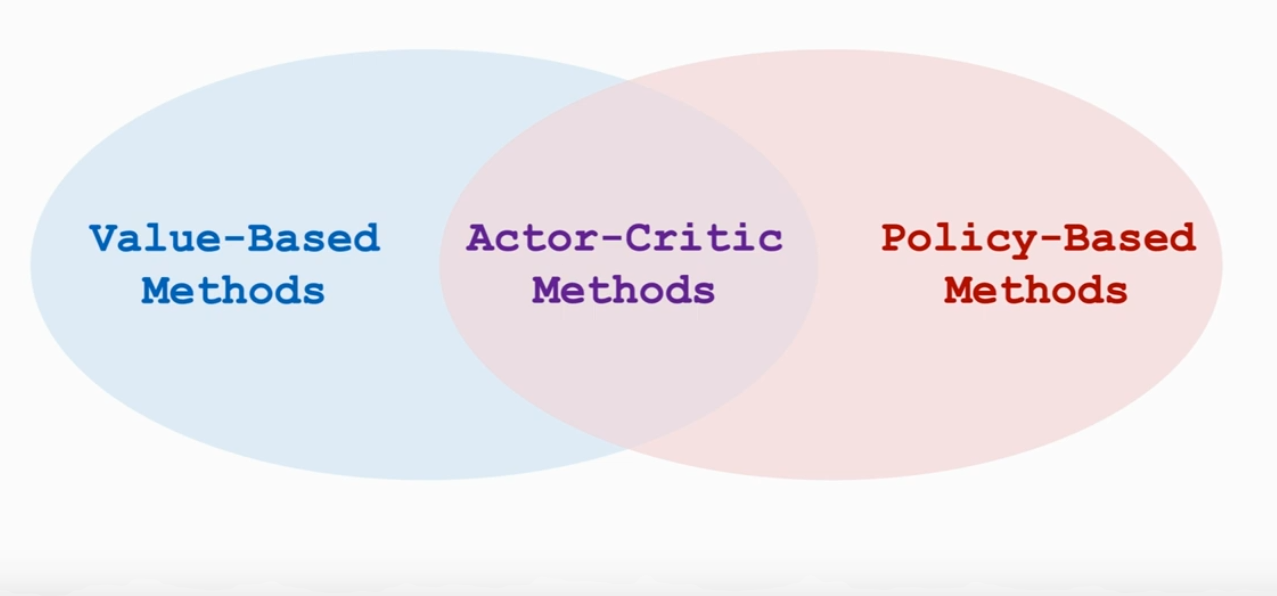
价值网络和策略网络(Value Network and Policy Network)
首先回顾状态价值函数 ,它是动作状态函数 的数学期望,如果动作是离散的,那么它是由策略函数 作为权重系数,和动作价值函数 (可以评价动作的好坏程度)相乘并对 a 做求和得到。如果动作是连续的,那么就要对 a 求积分。
①Policy network(Actor): 控制 Agent 运动,即在某一状态 s 做出动作 a
我们利用策略网络 来近似策略函数 , 是一个可训练的神经网络参数。
②Value network(Critic): 不控制 Agent 运动,仅给 Agent 打分
我们利用价值网络 来近似价值函数 ,w 是一个可训练的神经网络参数

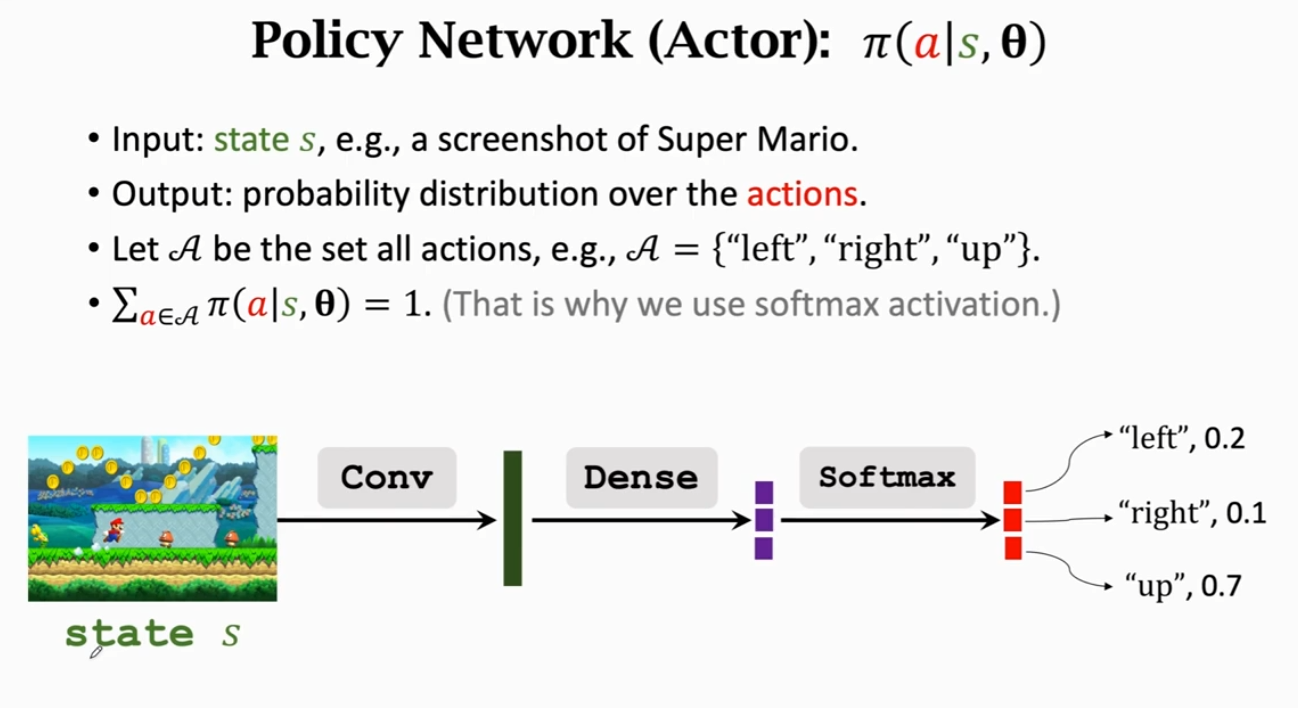
策略网络(Policy Network)(Actor)
以��超级玛丽为例:
该网络有一个输入:状态 s
将超级玛丽的一帧画面传输到策略网络中,即输入一个状态 s。
价值网络中包含:一个卷积层,将一帧画面变成特征向量;全连接层,将特征向量转变为相对于动作空间(Action Space)中元素个数对应的向量;再采用 Softmax 激活函数将其转换为求和为 1 的值,即一策略的概率密度。
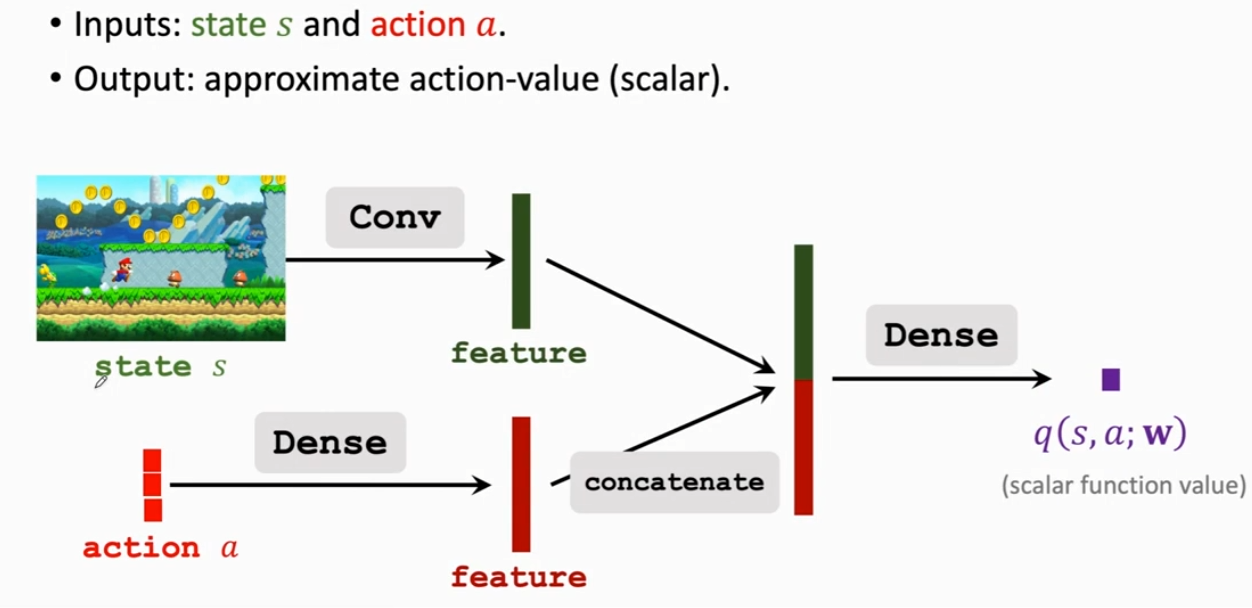
价值网络(Value Network)(Critic)
以超级玛丽为例:
该网络有两个输入:状态 s 和动作 a
将超级玛丽的一帧画面传输到价值网络中,即输入一个状态 s;以及策略网络(Actor)做出的一个动作 a 传入到价值网络中,即输入一个动作 a。对于离散动作而言,这里可以采用独热编码(one-hot encoding),具体可以参考 学习笔记 | 独热编码(One-Hot Encoding),这里不再对独热编码进行过多介绍。
对于两个不同的输入,处理方法如下:
针对于状态 s,采用一个卷积层,从输入中提取特征,获得一个状态特征向量
针对于动作 a,采用一个全连接层,从输入中提取特征,获得一个动作特征向量
然后将两个特征向量进行拼接,得到一个更高维的特征向量,再通过一个全连接层输出一个实数 ,即 Critic 对于 Agent 处于状态 s 下做出动作 a 的评价。
值得一提的是,价值网络和策略网络中的参数是可以共享的;当然,其中的参数也可以各自独立。
同时训练价值网络和策略网络就是 Actor-Critic Method(AC Method)
训练神经网络(Train the Neural Network)
因此,我们可以用策略网络和价值网络来近似状态价值函数。
针对于两个网络的参数 和 w,我们的更新方法是不一样的:
对于 ,它是策略网络的参数。我们更新参数 是为了让状态价值函数 的值增加, 是对策略 和状态 s 的评价。如果固定状态 s,那么 越大,意味着策略 越好;同理,如果固定策略 , 越大,则状态 s 越好。
对于 w,它是价值网络的参数。我们更新参数 w 是为了让价值网络对于动作的打分更精准,从而更好地估计未来奖励的总和。它相当于是裁判,一开始并没有打分能力,因此在初始阶段,Critic 的打分都是瞎猜的,它会通过环境给的奖励 Reward 来更新 w,最后 Critic 的打分会越来越精准。

利用如下五个步骤来对两个神经网络做一次更新:

使用时序差分算法更新价值网络 q(Update Value Network q Using TD)
解释一下,流程大概是这样的:
当我们使用 TD 算法去更新价值网络 q 时,要首先获取到 Actor 给出的 t 时刻和 t+1 时刻的状态 、 以及动作 at、at+1,此时 Critic 网络中的参数为 wt。因此我们就能得到我们的 TD target:,有了 TD target 和 t 时刻的观测值,即可写出 Loss L(w),且以 L2 范式形式表示,然后利用梯度下降(Gradient Descent)去更新 Critic 网络中的参数 w,记为 wt+1。需要注意的是,Agent 并不会做出 at+1 这个动作,仅仅是用于 Critic 用于 TD 算法的参数更新
直接附图:

使用策略梯度更新策略网络 (Update Policy Network Using Policy Gradient)
首先回顾一下策略梯度:
策略梯度是对自定义函数 g(A, θ)关于 A 求期望,由于一个 g(A, θ)是对整体的 g(A, θ)的一个无偏估计,因此这里用了蒙特卡洛近似。

解释一下,流程大概是这样的:
根据策略 对动作 a 进行一次随机抽样,然后针对该动作 a 进行一次随机梯度上升(Stochastic Gradient Ascent SGA),用于更新 ,记为 θt+1。

AC 方法的整体流程和对应关系:
算法总结(Summary of Algorithm)
直接上图,非常清晰:

值得注意的是,在论文和教科书中,最后一步往往不适用 qt,而采用的是 TD error 。使用 叫做基线策略梯度(Policy Gradient with Baseline),其效果更好。好的 baseline 可以降低方差,使算法收敛更快。
Baseline:任何接近 qt 的数都可以是 baseline,但它不能是 的函数,即不与 存在映射关系。
总结(Summary)


蒙特卡洛算法 Monte Carlo Algorithms
蒙特卡洛树搜索(Monte Carlo Tree Search)
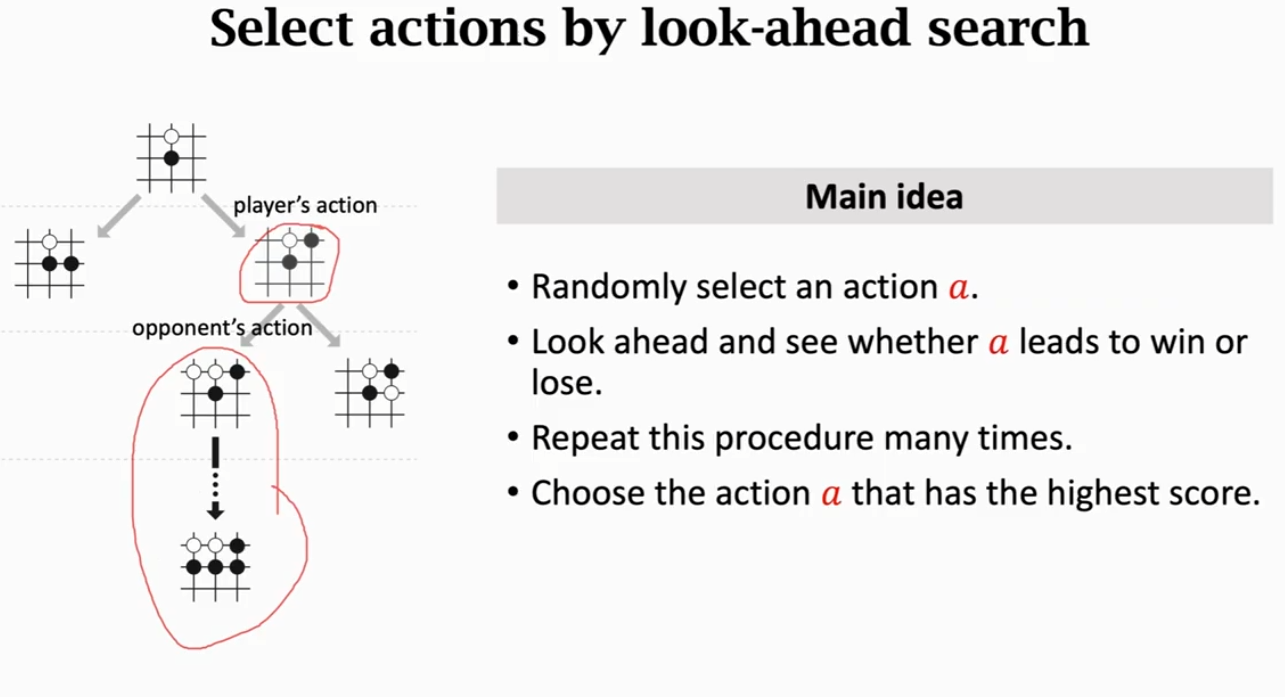
举个例子:人类在下棋的时候,必须多看几步,做出可能的结果

因此蒙特卡洛树搜索的主要思想是:
① 首先选取一个动作 a(这里选取的是一个相对较好的动作)
② 然后观测这个动作 a 能否致胜
③ 多次重复这个步骤
④ 选择最高分数的动作
蒙特卡洛树搜索的每次模拟都包含这四步:
① 选择 Selection: Agent 做出一个动作 a(这个动作是一个假想的动作,并不会让 Agent 实际做出动作)
② 拓展 Expansion: 对手会根据策略 做出一个动作,随后状态更新(同样也是一个假想的动作,且动作是由策略网络 所决定的)
③ 评估 Evaluation: 价值网络会对这个状态和动作进行打分,记作 v。同时,完成一个 trajectory 后(即完成一次对局)获得的奖励(Reward)记作 r。对该动作 a 进行标记分数
④ 更新 Backup: 用步骤 ③ 中标记动作分数的值来更新动作分数

具体步骤如下:




应用一:计算 (Application 1:Calculating )
在开始正式的蒙特卡洛方法开始前,先使用蒙特卡洛方法去计算圆周率 作为引子。
实际上,我们已经知道了 ≈3.141592653589...但我们能否使用随机数生成器去近似获取圆周率 呢?
接下来我们使用蒙特卡洛方法去近似生成 :
给定一个正方形,中心为原点,边长为 2。因此其中包含了一个单位圆。学过概率论的朋友会通过古典概型得知:这个概率显然是用圆的面积去除以正方形的面积。
这里假设是在正方形中进行 n 次随机抽样,那么对于这 n 次抽样,我们知道它的期望是 ,这是由于 n 次独立的随机抽样而得到的。

我们均匀的随机抽样 m 个点,如果 n 是一个很大的数,那么 m 也就越来越接近 π*n/4。通过移项,就可以得到 。
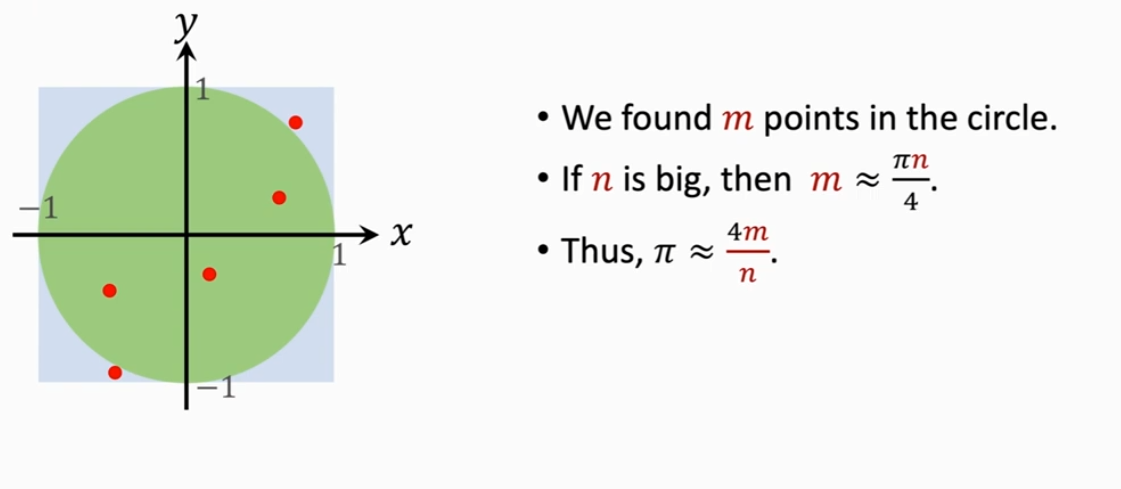
利用大数定律,可以知道当 n 趋于无穷时,4m/n 也趋于 。

结论如下:

应用二:蒲丰投针(Buffon's Needle Problem)
可以参考这篇文章 【概率论】蒲丰投针问题,具体不再过多赘述。
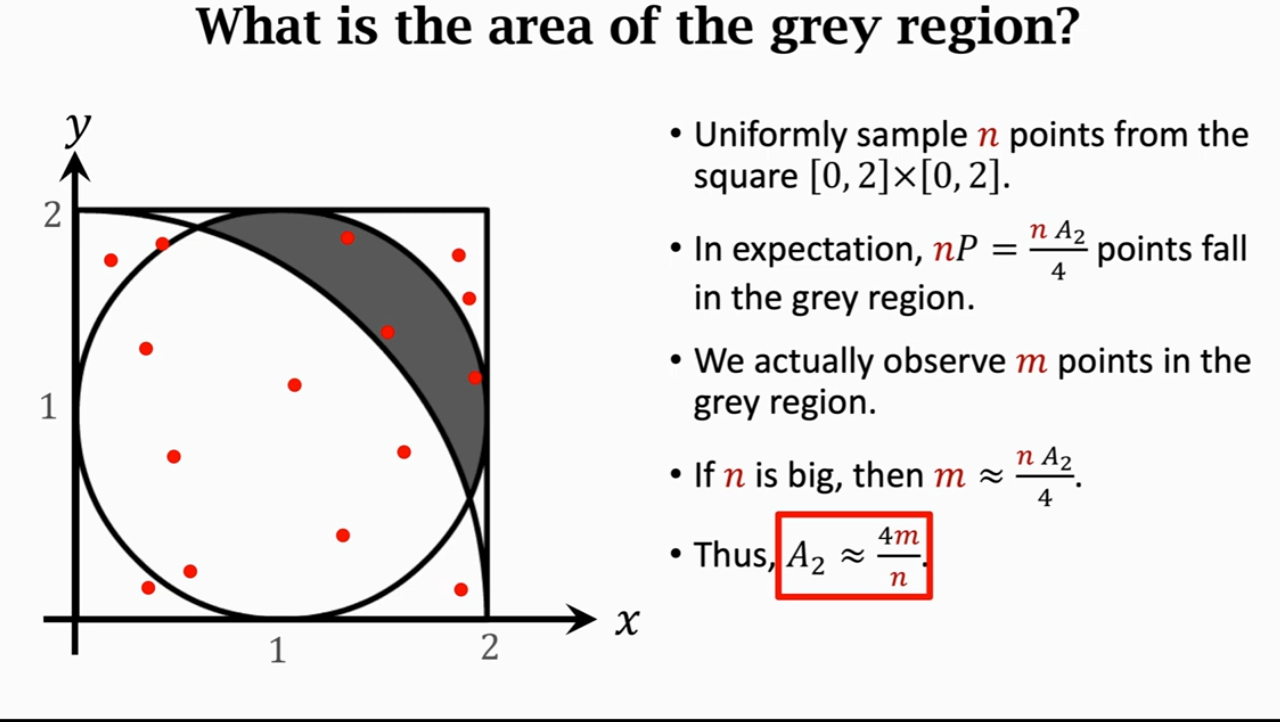
应用三:阴影面积估计(Area of A Region Estimation)
与应用一类似:在正方形中随机采样 n 个点,那么就能将落在阴影区域内的期望求出来。我们实际观测到了 m 个点在这个阴影区域。如果 n 很大,那么 m 就近似等于它的期望。通过移项,将阴影区域的面积 A2 算出来。
应用四:求积分(Integration)
蒙特卡洛方法近似求积分在工程上有十分重要的应用,例如对于某个函数 f(x)的积分,就可以采用如下的蒙特卡洛方法。
① 一元函数�的定积分

② 多元函数的定积分

应用五:期望估计(Estimate of Expectation)
非常重要!!!

SARSA 算法
推导 TD Target(Derive TD Target)
首先回顾一下折扣回报(Discounted Return),其中 是折扣率
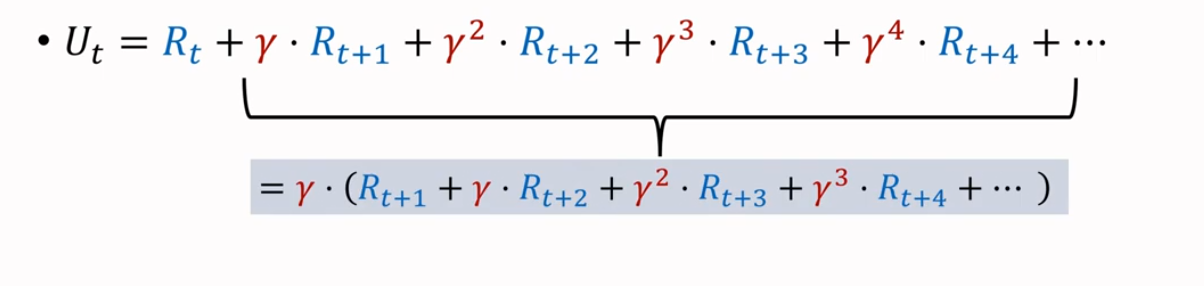
当我们提取出一个 ,会发现有如下等式,且括号内部的是下一步的折扣回报
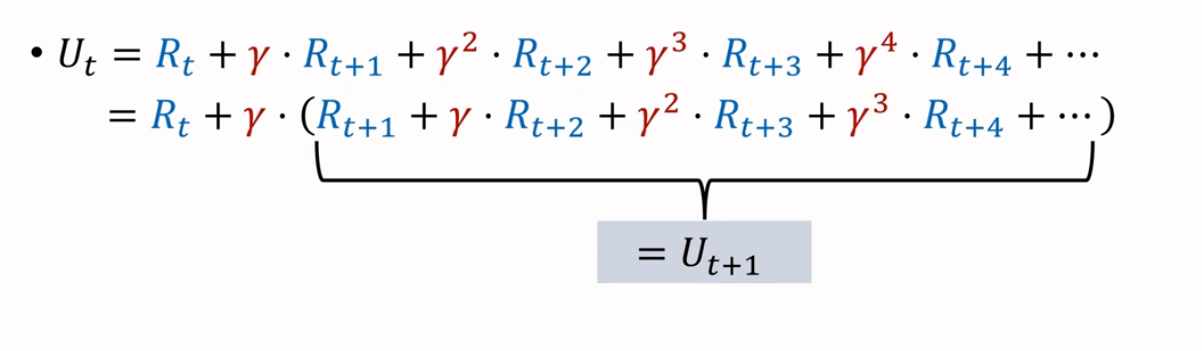
由此,我们得到了一个等式,来反映相邻两个回报之间的关系

我们通常认为,奖励 取决于当前的状态 ,当前的动作 at 以及下一状态
根据定义,我们可以得到 是回报 Ut 的条件期望,这里利用上述公式代换掉 Ut,那么就可以得到如下式子:

也许会有问题,博主在看的时候也有这个问题。对 Ut+1 求期望不已经是 了么,但实际上是这样的: 是期望,期望是对 这些变量求的,所以 跟这些变量无关。 还依赖于变量 。 进一步消掉 这两个变量。
因此我们可以得到这样的等式:
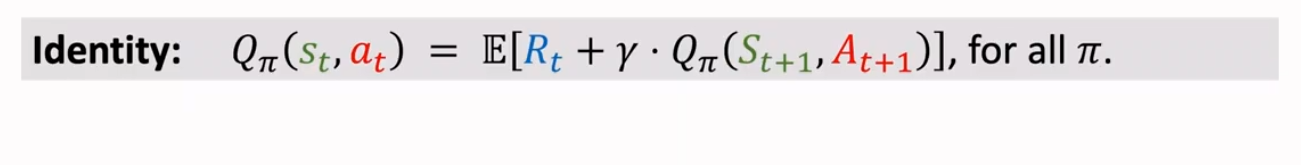
近似方法如下:
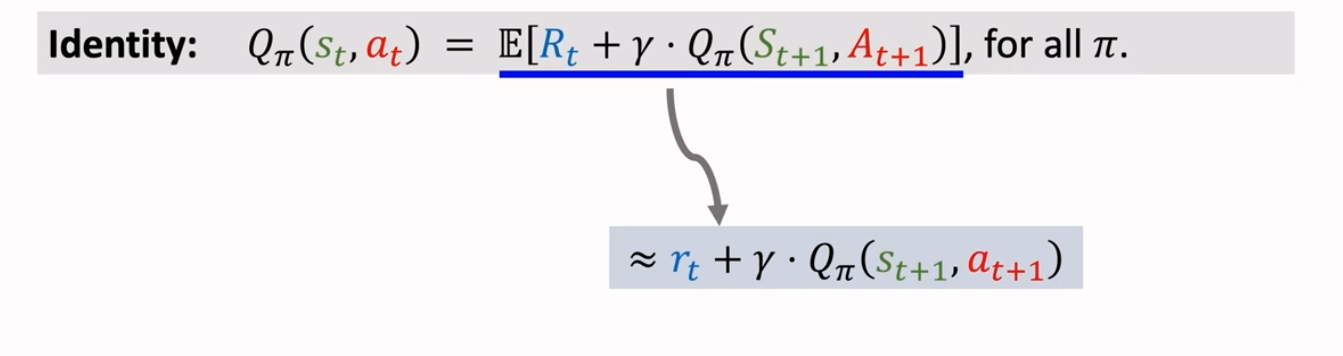
因此,TD learning 就是让 不断接近我们的 TD target

表格形式的 Sarsa(Sarsa:Tabular Version)
如果我们想学习动作价值函数 ,我们可以使用一个如果输入的状态和动作是有限的,那么我们就可以画一个表格:一行对应一个状态 ,一列对应一个动作 ,那么表中的每个元素则对应着在该状态和该动作下的动作价值 。我们要做的就是用 Sarsa 算法去更新表格,每次更新一个元素。
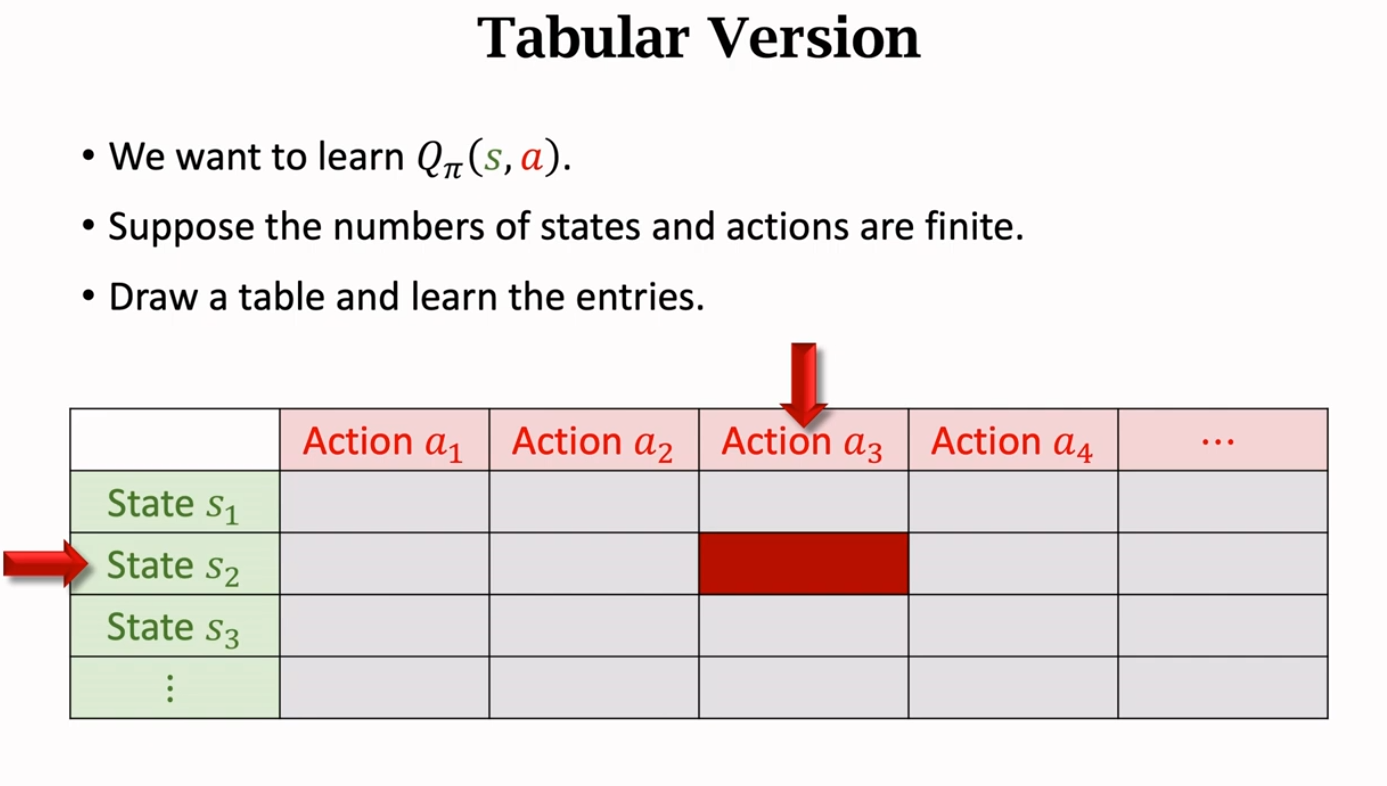
当我们观测到一个四元组 ,这样的一个四元组被称为 transition。然后采用策略函数 去采样一个 ,接着计算 TD target 。这里假设 为 , 经过采样为 ,那么我们经过查表获取到了对应的 。

同时我们也能计算出 TD error δt
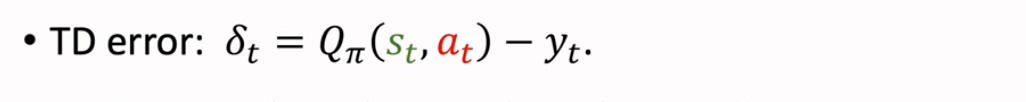
然后利用 δt 更新 ,其中 α 是学习率
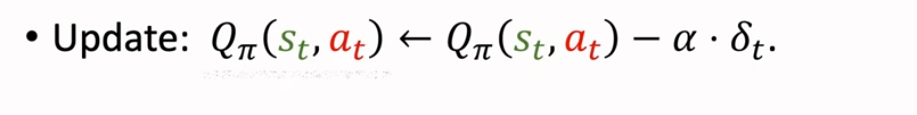
神经网络形式的 Sarsa(Sarsa: Neural Network Version)
我们可以采用价值网络来近似 ,记为 。注意,动作价值函数 和价值网络 q 都与策略 有关,策略 的好坏会影响这两个函数。
神经网络 被称为价值网络,它的输入是一个状态 s,输出是状态 s 下对应动作的价值。如果有 n 个动作,那么价值网络 q 就会输出一个 n 维向量,向量元素对应在状态 s 下,各动作 a 的价值。
TD target,记作 ,是实际观测的奖励 rt 与折扣价值网络的预测值 之和
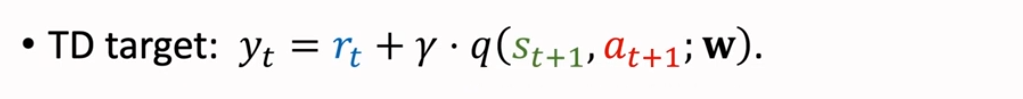
TD error,记作 δt,是价值网络对当前状态和动作的估计 与 TD target 之差,我们希望它越小越好
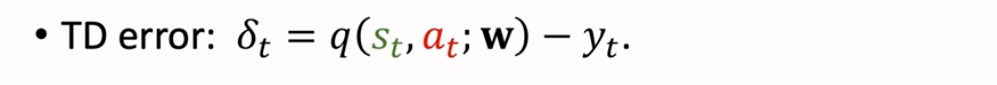
Loss,记作 L,以 1/2 倍 δt 的 L2 范式作为 Loss,我们希望通过更新价值网络的参数 w 来减小 Loss

Gradient,Loss 对 w 求梯度,利用梯度下降来获取到 Loss 的局部最小值
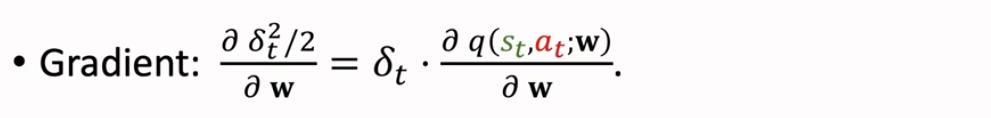
Gradient descent,梯度下降算法,用于更新价值网络参数 w
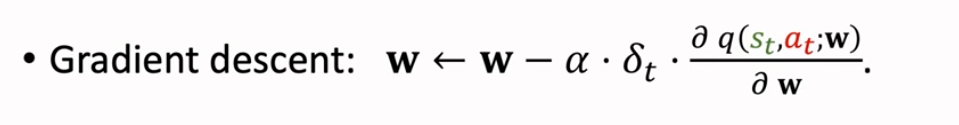
总结(Summary)
我们采用 Sarsa 算法主要是用于学习动作价值函数
这里有两种形式:
① 表格形式(直接学习 )
这种形式对于有限个状态和动作且数量不大。通过一张表格记录每种状态和动作对应的 的值,通过采用 TD 算法更新表中每个 的值。
② 神经网络形式(采用函数近似)
这种形式并不是直接获取 ,而是通过价值网络 来近似动作价值函数 。它实际上 TD 算法来更新价值网络参数 w,使价值网络 更好。应用有 学习笔记 4 的 AC 算法中的 Critic 网络。

Q-Learning 算法
Sarsa 算法与 Q-Learning 算法对比
Sarsa 算法
①Sarsa 算法目的是为了训练动作价值函数
②TD Target 记作 yt,它是当前观测到的奖励 rt 和动作价值函数对于下一状态和下一动作的预测值乘以折扣因子 γ 之和
③ 我们使用 Sarsa 算法来更新价值网络,即 AC 算法中的 Critic 网络。

Q-Learning 算法
①Q-Learning 是用于学习最优动作价值函数
②TD Target 记作 yt,是当前观测到的奖励 rt 与价值函数对于下一步状态下最优动作的预测值乘以折扣因子 γ 之和
③ 我们用 Q-Learning 算法来更新 DQN

推导 TD Target(DeriveTD Target)
我们已经知道对于所有的 π,已经有了如下的等式:
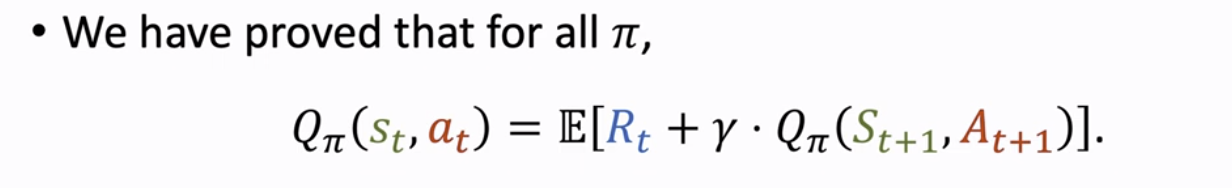
如果这里的 π 是最优策略 π*,那么就会有如下的等式:
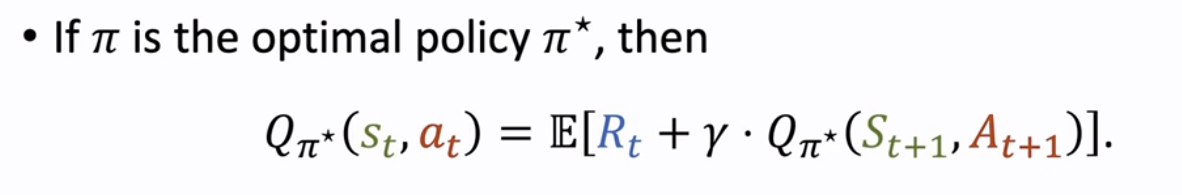
我们往往采用 去替换 Q_π*,因此有了如下的等式:

我们推导一下这个式子,由于 是对下一步状态下最优动作的动作价值函数,因此,这里的 必然要选择使 最大化的动作 ,因此有了如下的结论:
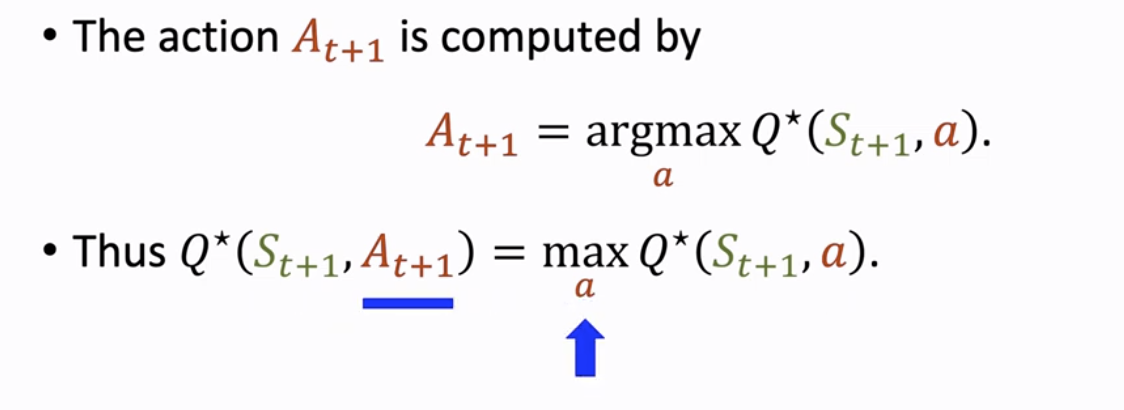
代入上面的等式,就可以得到如下等式:
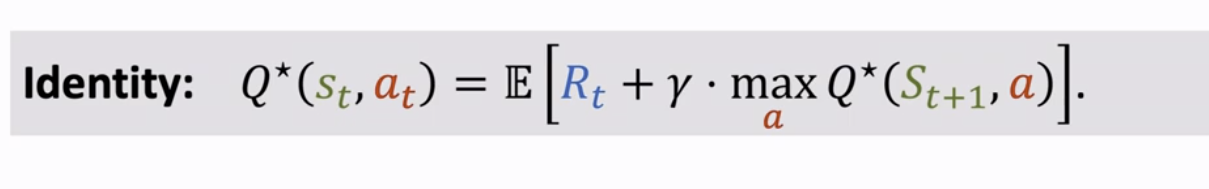
然而,直接求式子中的期望十分困难,因此这里采用蒙特卡洛近似:
将 Rt 近似为观测到的 rt,用观测到的下一状态 去近似 ,因此蒙特卡洛近似后的式子如下:
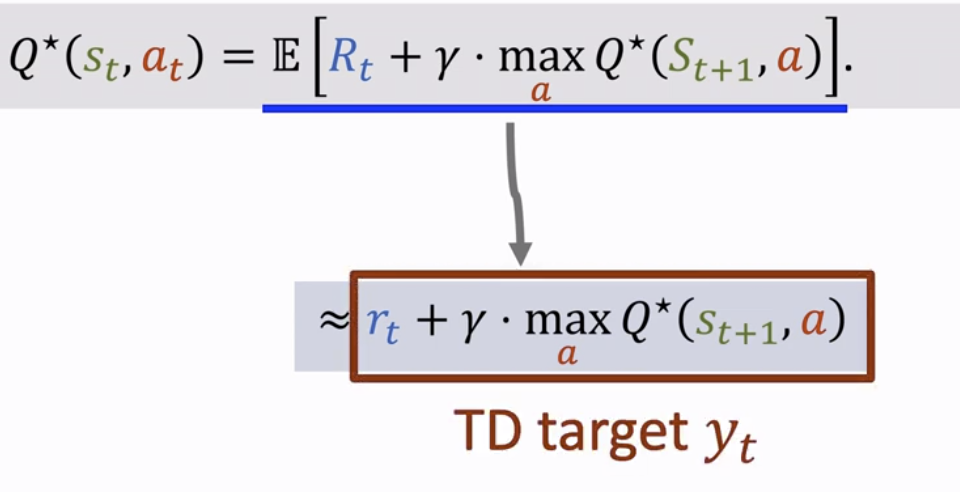
至此,我们得到了 TD Target yt
表格形式的 Q-Learning(Q-Learning:Tabular Version)
具体步骤如下
① 观测到一个四元组 ,这里称之为一个 transition

② 我们在上一节已经推导出 TD Target。实际上,这里的 Q 是一张表格,我们要找到对应的状态 并找到最大的动作价值函数 , 用于计算 TD Target yt。

③ 接下来,我们计算 TD error δt
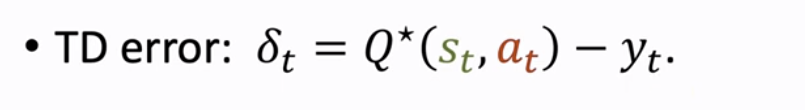
④ 最后,我们利用如下公式来更新表格中的 Q*(st, at)
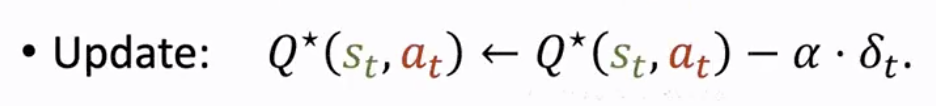
神经网络形式的 Q-Learning(Q-Learning:DQN Version)
我们采用 DQN 来近似最优动作价值函数
DQN 采用如下公式来控制 Agent,而我们就是帮助 DQN 来学习到更好的神经网络参数 w

具体步骤如下:
①
观测到一个四元组 ,这里称之为一个 transition

②TD Target yt,与上一小节类似,这里只是将表格中的 Q(st+1, a)换成了 Q(st+1, a*; w)
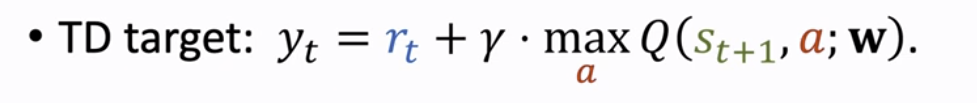
③TD error δt 类似
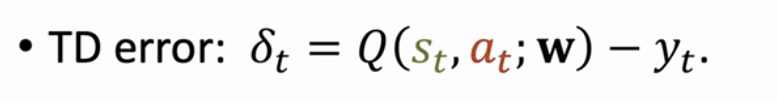
④ 最后,我们采用梯度下降来更新神经网络参数 w
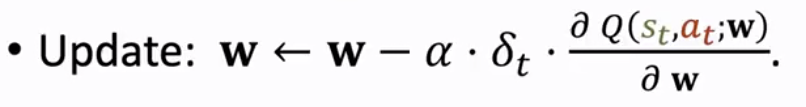
总结(Summary)
这里要注意 Q-Learning 与 Sarsa 的区别:Sarsa 算法是学习动作价值函数 ;而 Q-Learning 是学习最优动作价值函数 Q*。一个是随机取一个动作 ,一个是取最大 Q 的 , 但其目的都是让 Agent 获得到更高的分数。

Multi-Step TD Target
Sarsa 算法与 Q-Learning 算法(Sarsa versus Q-Learning)
Sarsa
①Sarsa 算法目的是为了 训练动作价值函数
②TD Target 记作 yt,它是当前观测到的奖励 rt 和动作价值函数对于下一状态和下一动作的预测值乘以折扣因子 γ 之和
③ 我们使用 Sarsa 算法来更新价值网络,即 AC 算法中的 Critic 网络。
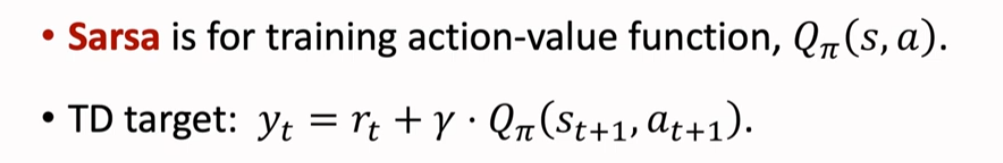
Q-Learning
①Q-Learning 是用于 学习最优动作价值函数
②TD Target 记作 yt,是当前观测到的奖励 rt 与价值函数对于下一步状态下最优动作的预测值乘以折扣因子 γ 之和
③ 我们用 Q-Learning 算法来更新 DQN。
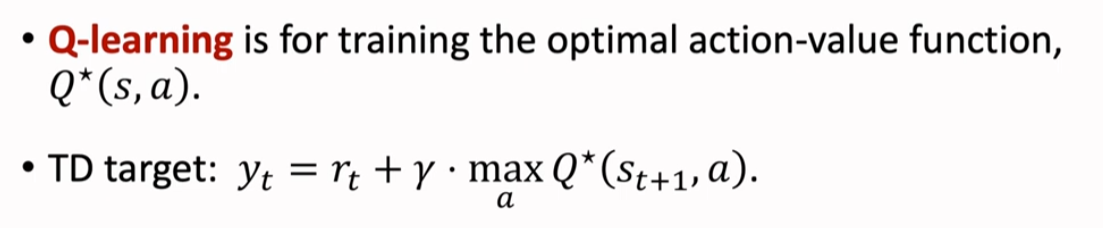
不管是 Sarsa 还是 Q-Learning,它们都只使用一个奖励 rt,即只使用一个 transition 中的奖励 rt,下一次使用另个 transition 来更新动作价值 ,这种方式算出来的 TD Target 叫做 One-Step TD Target。
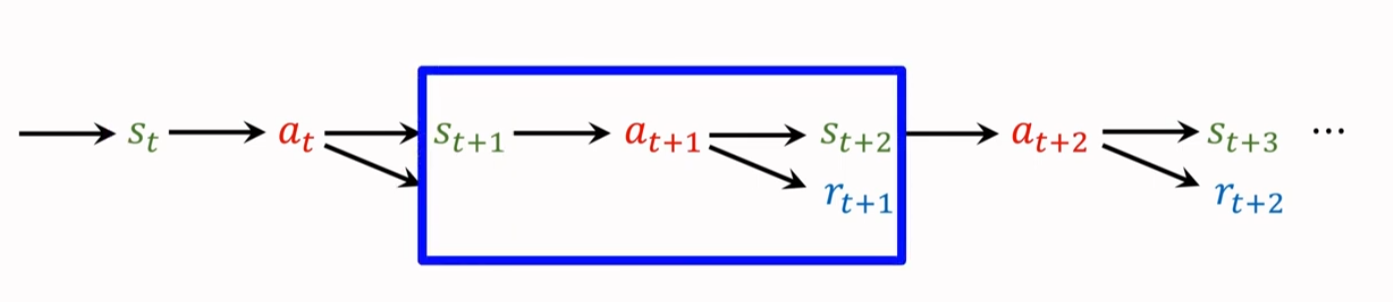
多步 TD Target(Multi-Step TD Target)
其实,我们可以使用多个奖励,如 rt, rt+1,即使用多个 transition 中的奖励去更新动作价值 ,这种方法计算出来的 TD Target 叫做 Multi-Step TD Target,
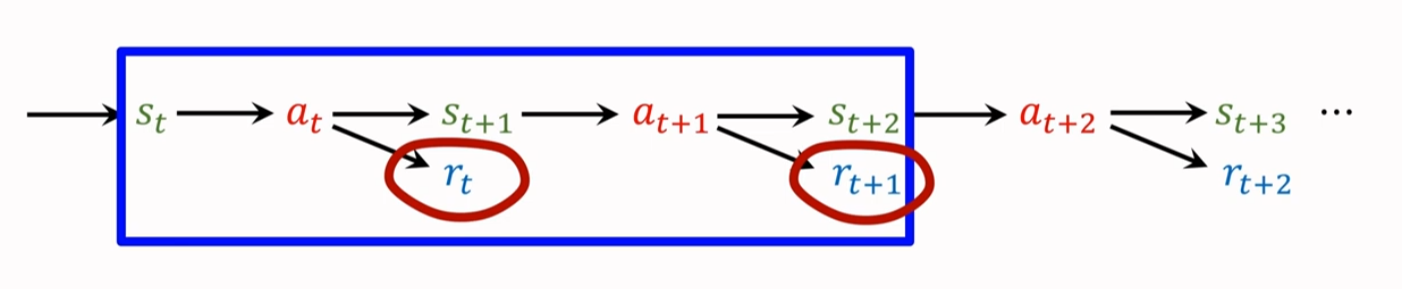
推导多步回报(Derive Mutil-Step Return)
我们已经知道的 Ut 与 Ut+1 的关系,然后再进行一次递归,将 Ut+1 用 Ut+2 表示,经过多步迭代,因而产生了 Ut 与 Ut+m 的关系,这个公式我们就称之为多步回报(Mutil-Step Return)

Sarsa 算法中的多步 TD Target(m-Step TD Target for Sarsa)
① 多步 TD target

② 若 ,即单步 TD target,也就是经典的 TD 算法

需要注意的是,这种单步的 TD Target 的训练效果往往不如多步的 TD Target 的训练效果
Q-Learning 算法中的多步 TD Target(m-Step TD Target for Q-Learning)
① 多步 TD target

② 若 ,即单步 TD target,也就是��经典的 TD 算法

需要注意的是,这种单步的 TD Target 的训练效果往往不如多步的 TD Target 的训练效果
单步 TD Target 与多步 TD Target 对比(Comparison of One-step TD target and Multi-step TD target)
Multi-Step TD target 的表现更好,更接近真实数据,偏差更小,结果也更稳定;而单步是多步的特例。

经验回放 Experience Replay
回顾深度 Q 网络和时序差分算法(Revisiting DQN and TD Learning)
Deep Q Network(DQN)
DQN 采用价值网络 来近似最优动作价值函数
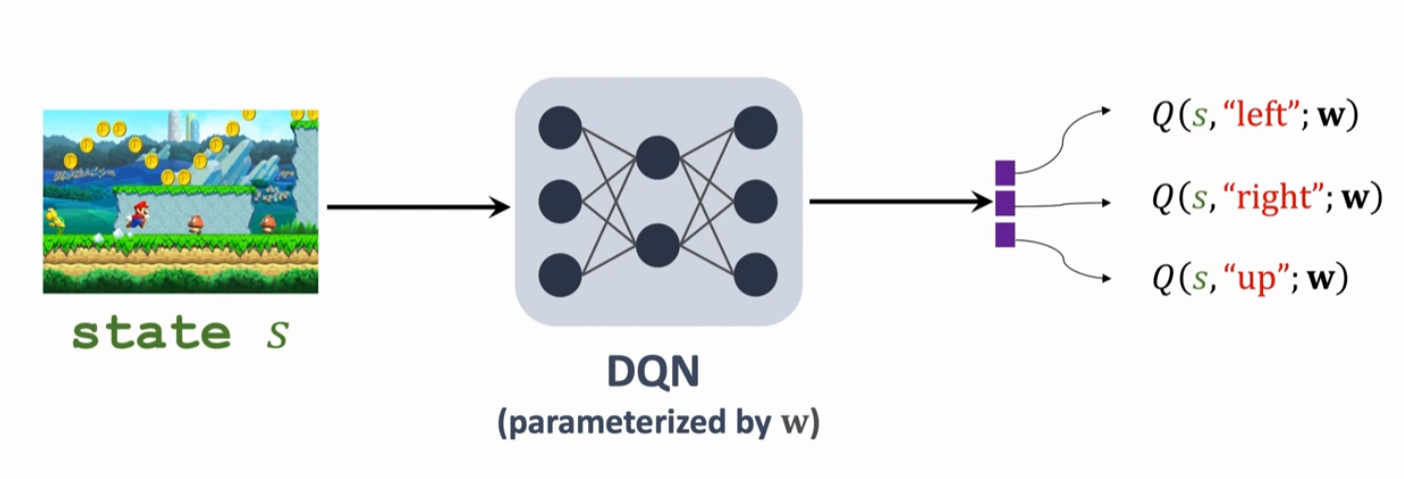
TD Learning
我们通常使用 TD 算法来训练 DQN,这里我们回顾一下 TD 算法的步骤:
①Agent 在 t 时��刻观测到一个状态 st 并做出动作 at
②Agent 与环境交互获得了一个新的状态 并且获得了一个奖励 rt
③ 此时,我们得到了 TD Target yt
④ 继而写出 TD error δt
我们的目标是让 qt 接近 yt,即使 TD error δt 尽量的小

因此 TD 算法就是寻找一个神经网络参数 w 使损失函数(Loss Function)L(w)尽可能的小
⑤ 采用梯度下降来使 wt 不断逼近

是一个四元组,这是一个 transition,可以认为是一条训练数据,传统算法在使用完该训练数据后就把它丢掉,不再使用,这种对于 DQN 的训练效果并不好。
为什么要使用经验回放(Why use the Experience Replay)
其实,关于讨论为什么要使用经验回放,其实就是在讨论不使用经验回放会有什么缺点,以及使用了经验回放有什么有点。
缺点一:浪费经验(Shortcoming 1:Watse of Experience)
传统的 TD 算法每次仅使用一个 transition,使用完后就丢掉,不再使用,这会造成浪费

缺点二:关联性更新(Shortcoming 2:Correlated Updates)
传统 TD 算法会按照顺序使用 transition ,前后两条 transition 之间有很强的关联性,即 st 和 非常接近,实验表明这并不利于把 DQN 训练的很好。

经验回放(Experience Replay)
回放缓冲区(Replay Buffer)
我们在使用完一个 transition 时,会把一个 transition 放入一个队列里,这个队列被称之为回放缓冲区(Replay Buffer),它的容量是一个超参数(Hyper Parameter)n,Replay Buffer 可以存储 n 条 transitions。
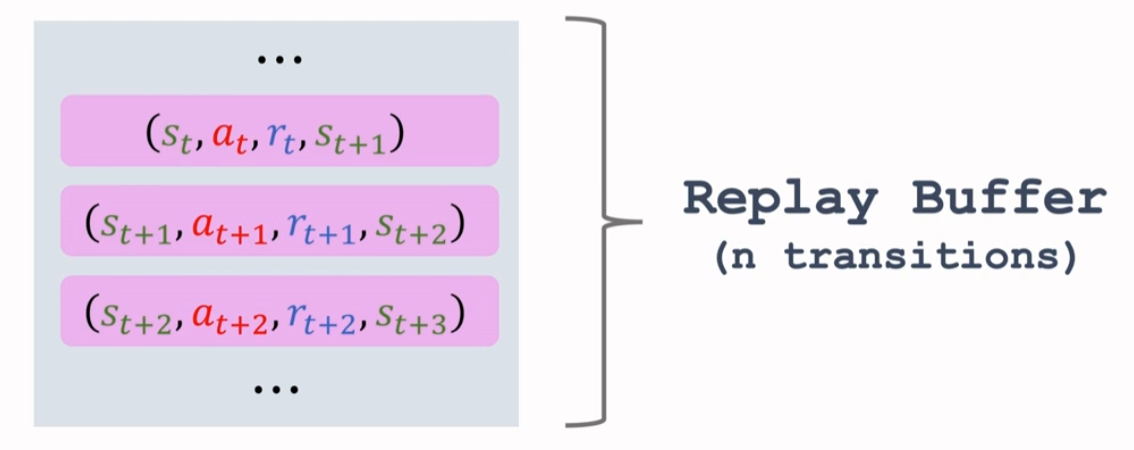
如果 Replay Buffer 满了,那么新来的 transition 会替代老的 transition

TD 算法中经验回放(TD with Experience Replay)
我们通过找到神经网络参数 w 来最小化损失函数 Loss Function。
我们是用随机梯度下降(Stochastic Gradient Descent SGD)来最小化损失函数 Loss Function:从 buffer 中随机抽取一个 transition(si, ai, ri, si+1), 然后计算 TD error δi,再算出随机梯度(Stochastic Gradient)gi,使用随机梯度下降(SGD)来调整神经网络参数 w。

值得一提的是,实践中,通常使用 mini-batch SGD, 即每次抽取多个 transitions,算出多个随机梯度,利用这多个随机梯度的平均来更新神经网络参数 w。
经验回放的优势(Benefits of Experience Replay)
① 打破了经验的相关性
② 重复利用过去的经验

优先经验回放(Prioritized Experience Replay)
基础思想(Basic Idea)
对于 Agent 而言,并不是所有的 transition 都是同等重要的。例如在超级玛丽游戏中,左侧的普通关卡和右侧的 boss 关卡,它们的重要性就不一样:普通关卡很常见,而 boss 关卡需要通过很多普通关卡后才能进行。因此,我们必须让 Agent 珍惜数量更少的 boss 关卡,即让 Agent 充分利用 boss 关卡的这一经验。

实际训练中,我们怎么样让 Agent 知道哪个 transition 是重要的呢?
可以使用 TD error 的 L1 范式,即|δt|来判断它的重要。|δt|越大,就说明 transition 就越重要,应该给这个 transition 更高的优先级。

解释一下:训练出的 DQN 对于数量较少的场景不熟悉,所以预测就会偏离 TD Target,因此产生的 TD error 就比较大,即|δt|就大。正因为 DQN 不熟悉数量较�少的场景,所以要让 DQN 给这些场景更高的优先级,让它更好的应对这样的场景。
核心想法(Core Idea)
优先经验回放(Prioritized Experience Replay)的核心在于:使用非均匀抽样代替均匀抽样。这里有两种抽样方式:
① 抽样概率 pt 正比于|δt|+ε
其中,ε 是一个很小的数,避免抽样概率 pt 等于 0

② 对|δt|排序
|δt|越大越靠前,|δt|越小越靠后

两种方法的原理都是一样的:|δt|越大,就抽样概率 pt 就越大。
调整学习率(Scaling Learning Rate)
TD 算法采用 SGD 来更新神经网络参数 w,α 是学习率。
如果做均匀抽样,那么所有的 transitions 的学习率 α 都相同;如果做非均匀抽样,那么就要根据每个 transition 的重要性来调整学习率。

如果一个 transition 有一个较大的抽样概率 pt,那么对这个 transition 的学习率就应该调小,可以采用如下圈出的方法来自适应调整学习率的因子:如果 pt 很大,那么学习率就会变小

4)更新 TD Error(Update TD Error)
为了做优先经验回放(PER),我们要对每一个 transition 标记上 TD error δt。δt 决定了这条 transition 的重要性,决定了它被抽样的概率。
如果一个 transition 刚刚被收集到,我们并不知道它的 δt,那么我们就直接把它的 δt 设置为最大值,让它有最高的优先级。
每次从 buffer 中抽取一个 transition,都要对它的 δt 进行一次更新

总结(Summary)
相比于传统的经验回放(ER),优先经验回放(PER)在每个 transition 中标注了 δt,并根据 δt 的不同来确定不同的抽样概率和学习率,从而达到非均匀抽样的效果。

置信域策略优化(Trust Region Policy Optimization,TRPO)
Optimization Basics
梯度上升(Gradient Ascent)
梯度上升是求取最大值所对应参数值的最简单的方法,只需要不断重复如下操作,就能让参数值不断逼近梯度最大的值。这里的问题是求最大值对应的参数值,采用了梯度上升。如果是求取最小值对应的参数值,那么就要采用梯度下降。

随机梯度上升(Stochastic Gradient Ascent)
使用梯度上升算法的前提是我们已经知道了目标函数 的关于变量 θ 的梯度。但有些情况下梯度是算不出来的。如下例:如果 是状态价值网络 V(S; θ)对于 S 求期望,求期望需要求取定积分,而定积分可能不存在解析解,因此我们求不出这个期望,所以我们无从得知梯度。
虽然求不出梯度,但我们可以求出随机梯度,随机梯度是对期望的蒙特卡洛近似。用随机梯度代替梯度,那么得到的算法就是随机梯度上升。随机梯度上升要重复下述三个步骤:

置信域(Trust Region)
我们用 来表示 的邻域。也就是一个集合,其中包含 附近所有的点,
下述的数学表达式表示: 是 θ 与 的 L2 范数距离 ,,如下图所示:

如果我们有一个函数,,且在邻域 内非常接近 ,那么 就被称为 置信域
需要注意的是, 仅在其 置信域 中与 非常接近,并不意味着在任何地方都与 接近

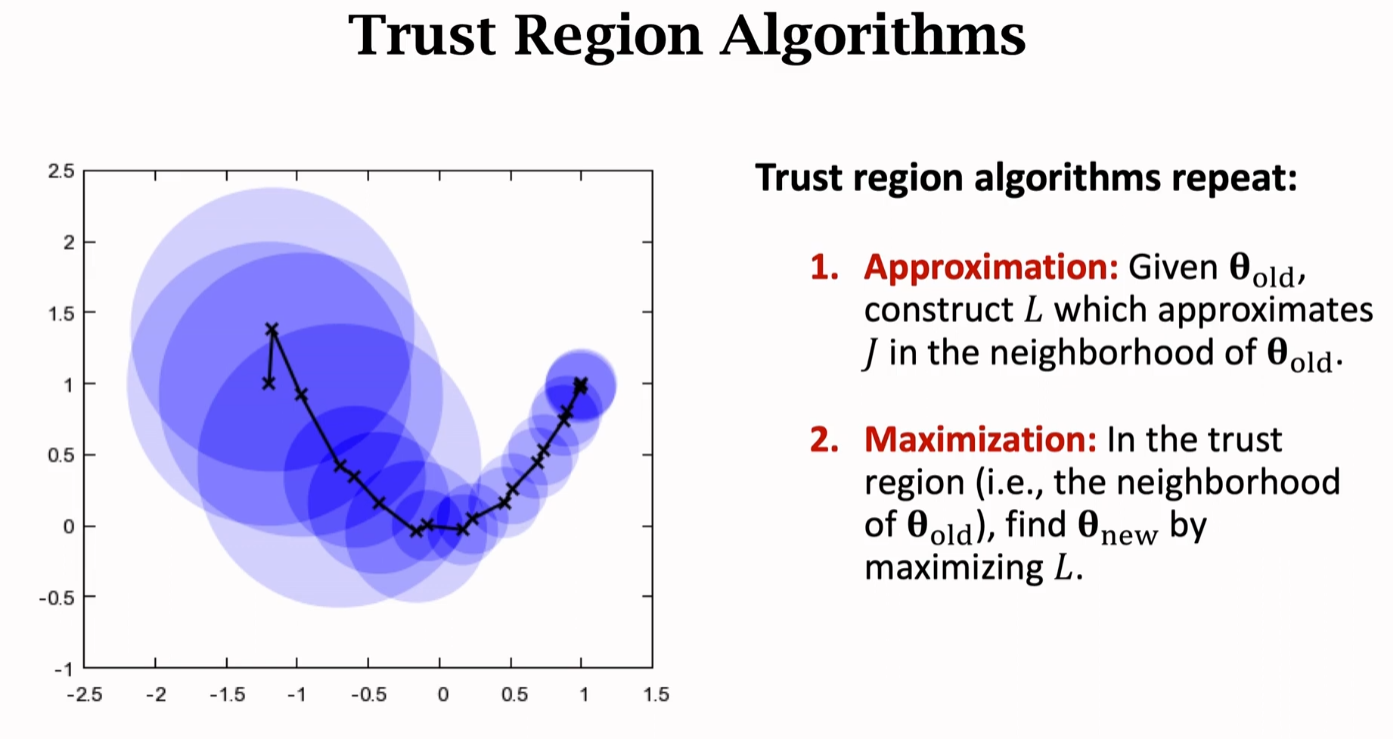
置信域算法(Trust Region Alforithms)
刚刚我们补充了 置信域(Trust Region),那么这里就要使用 置信域 的性质,即在置信域中,我们人为构造的函数 非常接近目标函数 ,因此我们可以在置信域内用 来代替 ,于是在置信域内能让函数最大化的点,也能让 最大化,这就是 置信域算法 的基本思路。置信域算法 就是多次重复这个步骤:

图中:蓝色圆圈代表置信域,黑线代表则是函数的方向。置信域的半径有可能改变。
Policy-Based Reinforcement Learning
首先回顾一下基础知识:

接下来做数学推导,将状态价值函数改写成其他形式:
如果将 作为概率密度函数,那么这个式子实际就是圈出部分的期望,期望是对动作 a 求的。

因此我们的目标函数就可以被替换成这样:

这个公式是 TRPO 最重要的公式!!!
Trust Region Policy Optimization(TRPO)
我们通常使用策略梯度算法来学习策略网络。策略梯度算法虽然很快,但它的表现并不稳定:一方面是对超参数的设置比较敏感:学习率设置对结果影响很大;策略梯度算法的随机性大,学习过程算法的表现波动非常大。策略梯度算法的收敛曲线通常会剧烈上下波动。
比起策略梯度算法,TRPO 的表现更加稳定。TRPO 对于超参数的设置不太敏感,算法的收敛曲线也不会剧烈波动。此外,TRPO 还有一个很好的优点:Sample Efficient, 也就是说观测到同样数量的奖励,TRPO 可以训练出更好的策略网络。

概括一下 TRPO:

Step 1:Approximation
已知变量 θ 当前的值为 ,我们对目标函数 在 处做近似。
这里的期望是对于状态 S 和动作 A 求的,把 S 和 A 看做随机变量

状态 S 的随机性来自环境的状态转移,状态转移是环境做的,我们不知道状态转移函数,因此我们可以把 Agent 实际观测到的状态看作成在环境中随机抽样得到的结果
动作 A 的随机性来自控制 Agent 的策略 π,Agent 实际的动作就是从��策略 π 中随机抽样得到的

实际就是让 Agent 与环境进行交互,获得一个 trajectory,因而就有如下推导:

所以我们利用 对 做近似:
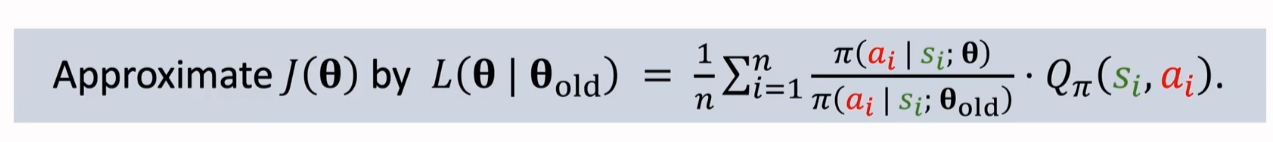
然而到这一步,我们仍然无法让 对 做近似。原因在于,我们并不知道动作价值函数 Qπ 是什么,因此我们要对动作价值函数 做近似。
这里使用观测到的折扣回报 来对 进行蒙特卡洛近似

至此,我们得到了构造函数 在 附近对于目标函数 的近似
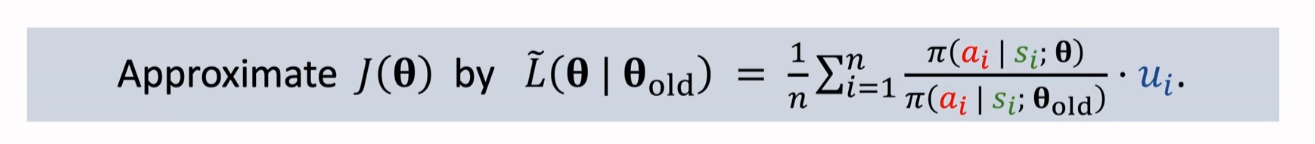
Step 2:Maximization
我们在求解最大化问题的时候,需要注意的是:这个最大化问题是有约束的
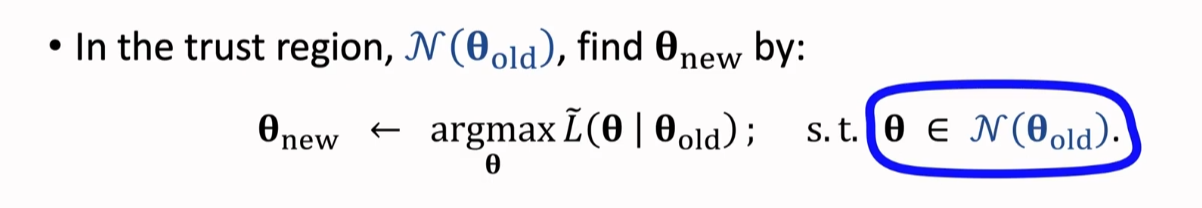
有了这个约束条件,那么即使第一步近似做的不够好,或者第二步最大化做的不够好,新的解 也不会离旧的解 太远,不至于让 θ 变得太糟糕。
这里有两种方法来衡量两者之间的距离:
让 θ 落在以 为圆心,△ 为半径的球中。
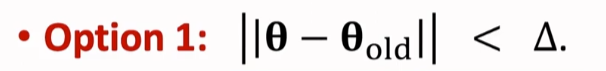
使用 KL Divergence 来衡量两个概率分布之间的距离,关于 KL Divergence 可以参考这篇博客 关于 KL 散度(Kullback-Leibler Divergence)的笔记。如果 θ 与 越接近,那么两个 π 输出的概率分布就会越接近,那么 KL Divergence 就会越小。所以使用 KL Divergence 的目的也是让新的 θ 不要离旧的 太远,新的参数 θ 要在旧的 邻域里(置信域)
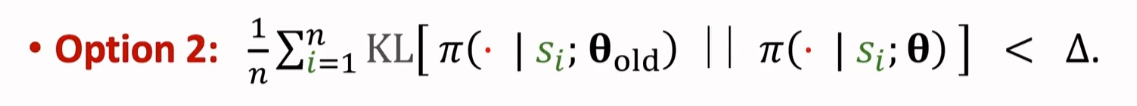
TRPO 总结(TRPO:Summary)
算法的第 1、2、3 步没有需要调节的超参数
算法的第 4 步,需要一个内循环,用梯度投影等方法来求解该优化问题。且有两个超参数,一个是梯度下降的步长,另一个是置信域的半径 △。但对 TRPO 的效果影响不大。

Policy Gradient Versus TRPO
直接附图:

PPO(TROP 简化改进版)
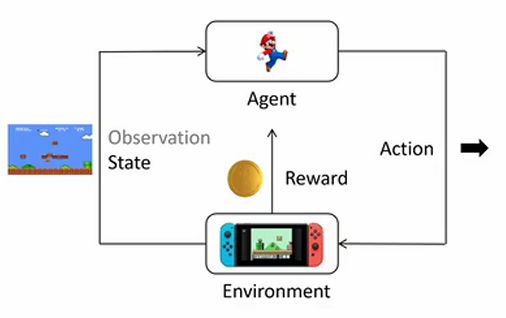
我们以超级马里奥游戏为例,逐步了解强化学习中涉及的基本概念:
- 环境 (Environment):环境是智能体所处的外部系统,它负责产生当前的状态,接收智能体的动作并返回新的状态和对应的奖励。环境的作用相当于模拟现实中的条件和反应规则,智能体只能通过与环境的交互来了解其动态变化。以超级马里奥游戏为例,环境包括玩家看到的游戏画面和后台程序逻辑。环境控制了游戏进程,例如生成敌人、提供奖励以及决定游戏何时结束。智能体并不知道环境的内部实现细节,只能依靠输入输出规则与环境互动。
- 智能体 (Agent):智能体是强化学习中的决策者,它会不断地观察环境的状态,并根据其策略选择动作。智能体的目标是通过选择一系列最优动作,获得尽可能多的累积奖励。
- 状态 (State):状态是环境在特定时刻的全面描述。对于智能体而言,状态是决策的基础,它包含了关于当前环境的所有重要信息。
- 动作 (Action):动作是智能体对当前状态的反应。基于当前的状态,智能体使用其策略函数来决定下一步要采取的动作。例如,在超级玛丽中,动作可以包括“向左移动”、“向右移动”和“跳跃”。动作可以是离散的(如跳跃或移动的方向选择)或者连续的(如机器手臂在三维空间中的移动角度)。强化学习的核�心在于使智能体学会如何在每个状态下选择最优的动作,从而最大化回报。
- 奖励 (Reward):奖励是环境对智能体执行动作后给予的反馈。奖励可以是正的(奖励)或者负的(惩罚)。例如,在超级马里奥游戏中,吃到金币可以获得正奖励(例如 +10 分),而碰到敌人会得到负奖励(例如 -100 分)。
- 动作空间 (Action Space):指智能体在当前状态下可以选择的动作集合。
- 轨迹 (Trajectory):轨迹(又称为回合或 episode)是指智能体在一次完整的交互过程中经历的一系列状态、动作和奖励的序列。轨迹通常表示为 ,其中 表示第 时刻的状态, 表示智能体在状态 下选择的动作。比如大语言模型生成时,它的状态就是已经生成的 token 序列。当前的动作是生成下一个 token。当前 token 生成后,已生成的序列就加上新生成的 token 成为下一个状态。
- 回报 (Return Reward):表示从当前时间步开始直到未来的累积奖励和,通常用符号 表示:。回报的定义是智能体决策的重要依据,因为强化学习的目标是训练一个策略,使得智能体在每个状态下的期望回报最大化。
强化学习的目标
在强化学习中,目标是训练一个神经网络 ,在所有状态 下,给出相应的 ,得到的 的期望值最大。即:
其中:
- :表示在策略 下轨迹 的回报 的期望值。
- :轨迹 的回报,即从起始状态到终止状态获得的所有奖励的总和。
- :表示一条轨迹,即智能体在环境中的状态和动作序列。
- :在参数 下生成轨迹 的概率,通常由策略或策略网络确定。
- :策略的参数,控制着策略 的行为。
所以,我们的目标是找到一个策略 ,使得 最大。那怎么找到这个策略呢?我们使用梯度上升的办法,即不断地更新策略参数 ,使得 不断增大。
首先,我们来计算梯度:
接下来,我们来看一下 Trajectory 的概率 是怎么计算的:
积分后得到:
-
:对轨迹 的概率对数进行求导,表示利用策略梯度对期望回报进行优化。
-
:表示轨迹 中所有步骤 上采取的动作 在状态 下的联合概率。
-
:利用对数的可加性,将联合概率的对数梯度分解为各步的对数梯度之和。
-
:对每一步动作的概率对数取梯度,分解为每一步的累加。
-
:利用累积回报 加权每一步的对数梯度,体现策略梯度方法中的优势估计。
-
:省略梯度符号后的形式,通常用于描述带有加权对数概率的情况。
那我们应该如何训练一个 Policy 网络呢?受局限我们可以定义 loss 函数为:
在我们的目标函数前加上负号,就可以转化为一个最小化问题。我们可以使用梯度下降的方法来求解这个问题。 但是,我们在实际训练中,通常会使用更加稳定的方法,即使用基于策略梯度的方法,例如 PPO、TRPO 等。
如以上公式所示,如果当前的 Trajectory 的回报 较大,那么我们就会增大这个 Trajectory 下所有 的概率,反之亦然。
这样,我们就可以不断地调整策略,使得回报最大化。
但这明显是存在改进空间的,因为我们只是简单地使用回报来调整策略,而没有考虑到回报的分布,这样就会导致回报的方差较大,训练不稳定。
针对这个问题,我们修改一下公式,首先对 求和:
其中:
-
:轨迹 的累积回报,这里使用了未来回报的折扣求和来表示。
-
:从时间步 开始的未来折扣回报,表示轨迹 在时间步 时的累计回报。
-
:对时间步 到 (轨迹结束时刻)之间的所有奖励进行求和。
-
:折扣因子 的幂次,控制未来奖励的权重,。当 越远离当前时刻 ,其贡献越小。
-
:在时间步 发生的即时奖励。
总的来说,修改后的公式是对未来回报的折扣求和,这样当前动作的概率就不再只取决于当前的回报,而是取决于未来的回报,这样就可以减小回报的方差,使得训练更加稳定。
还有一种情况会影响我们算法的稳定性,那就是在好的局势下和坏的局势下。比如在好的局势下,不论你做什么动作,你都�会得到正的回报,这样算法就会增加所有动作的概率。得到 大的动作的概率大一些,但是这样会让训练很慢,也会不稳定。最好是能够让相对好的动作的概率增加,相对坏的动作的概率减小。
为了解决这个问题,我们可以对所有动作的 reward 都减去一个 baseline,这样就可以让相对好的动作的 reward 增加,相对坏的动作的 reward 减小,也能反映这个动作相对其他动作的价值。
所以我们的目标函数就变为:
其中, 也需要用神经网络来拟合,这就是我们的 Actor-Critic 网络。Actor 网络负责输出动作的概率,Critic 网络负责评估 Actor 网络输出的动作好坏。
接下来我们再来解释几个常见的强化学习概念:
-
Action-Value Function: 每次都是随机采样,方差很大,我们可以用 来代替, 表示在状态 下采取动作 的价值,即从状态 开始,采取动作 后,按照某个策略 执行,最终获得的回报的期望值。 可以用来评估在状态 下采取动作 的好坏,从而指导智能体的决策,即动作价值函数。
-
State-Value Function: 表示在状态 下的价值,即从状态 开始,按照某个策略 执行,最终获得的回报的期望值。 可以用来评估在状态 下的好坏,从而指导智能体的决策,即状态价值函数。
-
Advantage Function:,表示在状态 下采取动作 相对于采取期望动作的优势。优势函数可以用来评估在状态 下采取动作 的优劣,从而指导智能体的决策,即优势函数。
有了这些概念,我们再回过头来看我们的目标函数:
其中: 就是我们刚刚讲的优势函数,表示在状态 下采取动作 相对于采取期望动作的优势。那我们的目标函数就变成了:最大化优势函数的期望。
那如何计算优势函数呢?我们重新来看一下优势函数的定义:
表示在状态 下采取动作 的价值, 表示在状态 下的价值。我们来看一下下面�这个公式:
其中:
-
:执行动作 后,在状态 下获得的即时奖励。
-
:折扣因子,用于确定未来奖励的重要性。折扣因子接近 1 时,更加关注未来的奖励;接近 0 时,更加重视即时奖励。
-
:价值函数,用参数 表示,估计下一个状态 的价值,即从该状态开始的预期未来奖励。
我们把上述公式代入到优势函数的定义中:
我们可以看到,现在优势函数中只剩下了状态价值函数 和下一个状态的价值函数 ,这样就由原来需要训练两个神经网络变成了只需要训练一个状态价值网络,这样就减少了训练的复杂度。
在上面的函数中,我们是对 Reward 进行一步采样,下面我们对状态价值函数也进行 action 和 reward 的一步采样。
接下里,我们就可以对优势函数进行多步采样,也可以全部采样。
从图片中提取的公式为:
我们知道,采样的步数越多,会导致方差越大,但偏差会越小。为了让�式子更加简洁,定义:
其中:
-
:是时间步 的优势函数,表示当前时刻 的即时奖励 加上下一个状态的折扣价值 减去当前状态的估计价值 。
-
:是时间步 的优势函数,类似地表示在时刻 获得的即时奖励 加上状态 的折扣价值 减去状态 的价值估计 。
那我们究竟要采样几步呢?介绍一下广义优势估计 GAE(Generalized Advantage Estimation),小孩子才做选择,我(GAE)全都要。
假如 :
将上面定义好的 和 代入到 GAE 优势函数中:
最终我们可以得到:
Proximal Policy Optimization (PPO)
PPO 是 OpenAI 提出的一种基于策略梯度的强化学习算法,它通过对策略梯度的优化,来提高策略的稳定性和收敛速度。PPO 算法的核心思想是在更新策略时,通过引入一个重要性采样比例,来限制策略更新的幅度,从而保证策略的稳定性。
PPO 算法目标函数(修正版)
PPO 算法的目标函数为:
其中:
- :对 条轨迹(采样的样本)取平均值。这里的 表示采样轨迹的总数,通过对多个轨迹求平均来估计梯度,以获得更稳定的更新。
- :对每条轨迹 中的 个时间步求和,表示对单条轨迹中的所有时间步的累积。
- :广义优势估计(Generalized Advantage Estimation, GAE),由参数 估计,用于计算在状态 下采取动作 的优势。
- :表示策略的重要性权重,其中分母 是旧策略(或目标策略),分子 是新策略的概率。对整个目标函数求导后可得到策略梯度,这个比值反映了新旧策略在同一状态-动作对上的相对概率密度,利用这一比值来更新策略参数 。
整个公式的作用是通过优势估计来构造策略梯度的目标函数,优化该目标函数可更新策略参数,使得策略倾向于选择优势更高的动作,从而提升策略性能。GAE 可以有效降低方差,使得策略优化过程更加稳定和高效。
将目标函数取负号,转化为最小化问题,我们可以得到:
具体来说,PPO 算法�主要包括两个关键的技术:Adaptive KL Penalty Coefficient 和 Clipped Surrogate Objective。
PPO-惩罚(PPO-Penalty)用拉格朗日乘数法直接将 KL 散度的限制放进了目标函数中,这就变成了一个无约束的优化问题,在迭代的过程中不断更新 KL 散度前的系数。即:
其中:
- :这是 KL 散度项,用于限制新旧策略之间的距离,其中 表示策略 和旧策略 之间的 KL 散度。超参数 控制 KL 散度项的权重,从而调节新旧策略之间的差异,防止策略更新过大导致不稳定。
整个 PPO-KL 损失函数的目的是通过限制新旧策略的差异(使用 KL 散度项)来优化策略,使其更稳定地朝着优势更高的方向进行更新。PPO 的这种约束策略更新的方法相比于其他策略优化方法更为稳定且有效。
PPO 截断(PPO-Clipped)是 PPO 的另一种变体,它通过对比新旧策略的比值,来限制策略更新的幅度,从而保证策略的稳定性。具体来说,PPO-Clipped 的目标函数为:
-
:裁剪函数,将概率比裁剪到 区间,防止策略的更新步长过大。这里 是一个超参数,控制裁剪的范围。
-
:在未裁剪的概率比项和裁剪后的项之间取最小值。这一操作的目的在于限制策略更新幅度,以防止策略偏离旧策略过远,从而导致不稳定的学习过程。
整个 PPO-clip 损失函数的作用是通过裁剪操作约束策略的变化幅度,使策略更新不会过于激进。这种方式相比于传统策略梯度方法更为稳定,并且在优化过程中能够有效平衡探索和利用。PPO2 的这种裁剪机制是其成功的关键,广泛用于实际的强化学习应用中。
好了,如果你坚持看到了这里,那想必你已经差不多掌握了强化学习的基本思想和 PPO 算法的基本思想。接下来你可以将 PPO 应用到大模型的训练中啦!
参考文献
DPO 是如何简化 RLHF 的
DPO本质上是SFT范畴,其推导假设了一个无最优解的loss为0,存在理论缺陷。走DPO路线的公司已有多家失败案例,并推荐了on-policy蒸馏等更优方法。大家一致认为,DPO虽然数据格式简单,但在数据量少的情况下效果有限,且其适用性要求严格。
强化学习基本功(方法论)
学习深度强化学习,最重要的基本功到底是什么?
如果你现在卡住,不知道该怎么继续深入学习下去,不是因为你学得不够多,不是因为你缺少知识,而是因为你缺坐标系。
第一条暴论:深度强化学习的第一基本功,不是算法,是问题建模能力
很多人一上来就问:DQN、PPO、SAC、TD3 到底该学哪个?参数怎么调?loss 为什么不收敛?
但现实是:90% 的强化学习失败,不是算法选错,而是问题根本就不该这么建模。
你有没有认真想过这些问题:
- 这个任务是不是马尔可夫的?
- 状态是不是信息不全?
- reward 有没有在误导 agent?
- 你是在学策略,还是在学 exploit bug?
如果你对这些问题没有感觉,那你学再多算法,都是在盲人调参。
强化学习真正的基本功,是把一个现实问题,压缩成一个“没那么烂”的 MDP。
这一步,比写网络结构难十倍,也重要十倍。
第二条暴论:数学不是为了推公式,而是为了让你知道什么时候该绝望
非科班出身的人,往往有两种极端:一种是恐惧数学,另一种是沉迷数学。
但在强化学习里,数学真正的价值只有一个:
- Bellman 方程告诉你:这是个自洽系统,不是玄学
- contraction mapping 告诉你:为什么 value iteration 能收敛
- stochastic approximation 告诉你:为什么你训练不稳定是常态而不是异常
你不需要能手推所有证明,但你必须能在训练崩掉的时候,分清楚:这是实现问题,还是问题本身就不可解。
不知道这一点的人,会把一年时间浪费在一个从一开始就不可能稳定的设定上。
第三条暴论:强化学习最硬的基本功,其实是实验素养
这是几乎所有新手都会忽略的一点。
强化学习不是 supervised learning,你没有 ground truth,你只有 trajectory、reward 曲线和一堆噪声。
这意味着什么?意味着你必须具备比其他方向 高一个数量级的实验控制能力:
- 固定随机种子
- 分离算法改动与环境改动
- 理解 variance 从哪里来
- 不被单次 run 欺骗
如果你看到 reward 曲线涨了,就开始兴奋,那我可以很肯定地说:你还没入门。
在强化学习里,不怀疑实验结果,本身就是一种不专业。
第四条暴论:代码能力不是会写,而是能活着 debug��
强化学习的代码,有三个特点:
- 状态流动复杂
- bug 不会立刻报错
- 错了也能“看起来在学习”
这对非科班的人极其不友好。你必须具备:
- 把算法拆成可验证模块的能力
- 用最小环境复现实验现象的能力
- 能从一条 trajectory 里反推 agent 在想什么的能力
很多人不是被算法难死的,是被模型在学,但不知道学了什么这种状态慢慢耗死的。
第五条暴论(最重要):强化学习真正的基本功,是心理素质
强化学习是所有 AI 方向里,回报延迟最长、反馈最差、挫败感最强的领域之一。
你会经历:连续一周 reward 不涨;改了十个超参,结果随机波动;别人的论文一跑就好,你的环境怎么都不行
如果你需要频繁的正反馈才能坚持,那这个方向会把你折磨得怀疑人生。
那你现在,到底该补什么?
不是再学一个新算法,而是反过来,补这几件事:
- 用一句话说清楚你的任务是不是一个合理的 MDP
- 能解释 reward 曲线每一个异常波动的可能原因
- 能回答“如果这个方法失败,我打算如何证明不是我实现错了”
- 能明确说出:这个问题,RL 相比 rule-based / optimization 到底优势在哪
action state reward 的作用
设计action space 接近于帮 LLM agent 的抽象出它的 skills
设计 state space 接近于帮 LLM 选择需要置入 上下文的内容或者写提示词
reward function 相当于帮LLM设计 evaluation 和verify 模块,直接决定 它的自行迭代环路的 转动速度